The Wicker Man (1973
Edit Storyline Sgt. Howie travels to Summerisle to investigate the disappearance of a young girl. He discovers that the locals are weird and unhelpful, and becomes determined to get to the bottom of the disappearance. Written by Sean Taylor <st52@cornell.edu>
Quantum chromodynamics
In theoretical physics, quantum chromodynamics (QCD) is a theory of strong interactions, a fundamental force describing the interactions between quarks and gluons which make up hadrons such as the proton, neutron and pion. QCD is a type of quantum field theory called a non-abelian gauge theory with symmetry group SU(3). The QCD analog of electric charge is a property called 'color'.
"May Reveal a Signal Created at Birth of Universe"
The Cosmic Microwave Background is the most ancient light that has traveled almost unimpeded across the Universe, and it contains a wealth of information about the origin and nature of the cosmos. During their journey, photons from the CMB have encountered a multitude of galaxies and galaxy clusters and have been deflected by these large concentrations of matter. This phenomenon, known as gravitational lensing, imprints a subtle distortion on the pattern of the CMB that encodes details about the large-scale distribution of structure in the Universe. In recent years, cosmologists have detected the signature of gravitational lensing on the CMB temperature using data from ground-based and space-borne experiments, including the first all-sky image of this effect achieved using ESA's Planck satellite. The image below shows the effect of gravitational lensing on the Cosmic Microwave Background.(Credit: G.
Complex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the real natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of a complex number z is a complex number w such that ew = z.[1] The notation for such a w is ln z or log z. Since every nonzero complex number z has infinitely many logarithms,[1] care is required to give such notation an unambiguous meaning. If z = reiθ with r > 0 (polar form), then w = ln r + iθ is one logarithm of z; adding integer multiples of 2πi gives all the others.[1] Problems with inverting the complex exponential function[edit] For a function to have an inverse, it must map distinct values to distinct values, i.e., be injective.
HomeschoolScientist
Upload TheHomeschoolScientist.com Subscription preferences Loading... Working...
Photoelectric effect
The photoelectric effect is the observation that many metals emit electrons when light shines upon them. Electrons emitted in this manner may be called photoelectrons. According to classical electromagnetic theory, this effect can be attributed to the transfer of energy from the light to an electron in the metal. From this perspective, an alteration in either the amplitude or wavelength of light would induce changes in the rate of emission of electrons from the metal. Furthermore, according to this theory, a sufficiently dim light would be expected to show a lag time between the initial shining of its light and the subsequent emission of an electron. However, the experimental results did not correlate with either of the two predictions made by this theory.
Chemistry with sorted molecules: Reaction rate of many molecules depends on their shape
Most molecules occur in several shapes, which may behave very differently. Using a sorting machine for molecules, a German-Swiss research team can now for the first time directly measure the various reaction rates of different forms of the same compound. The team, led by DESY scientist Prof. Jochen Küpper from the Hamburg Center for Free-Electron Laser Science CFEL and Prof.
Abstract algebra
The permutations of Rubik's Cube have a group structure; the group is a fundamental concept within abstract algebra. History[edit] As in other parts of mathematics, concrete problems and examples have played important roles in the development of abstract algebra. Through the end of the nineteenth century, many -- perhaps most -- of these problems were in some way related to the theory of algebraic equations. Major themes include: Numerous textbooks in abstract algebra start with axiomatic definitions of various algebraic structures and then proceed to establish their properties.
drawstuffrealeasy
Upload ShooRaynerDrawing Channel Subscription preferences Loading... Working... drawstuffrealeasy
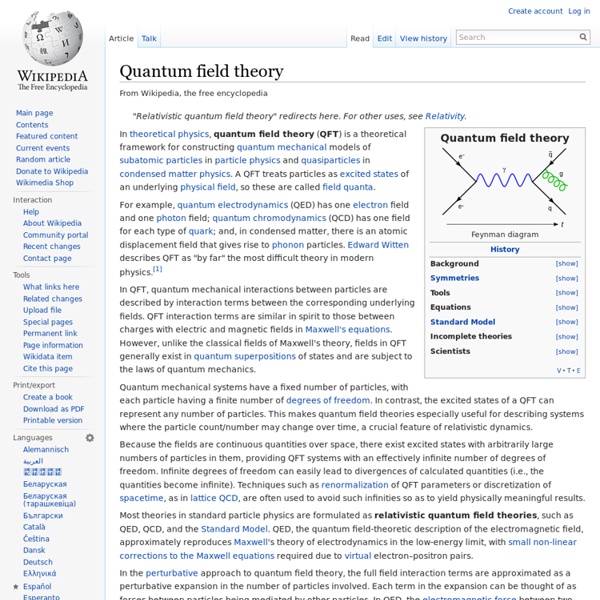
Quantum electrodynamics
In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction. History[edit] The first formulation of a quantum theory describing radiation and matter interaction is attributed to British scientist Paul Dirac, who (during the 1920s) was first able to compute the coefficient of spontaneous emission of an atom.[2]