Golden Ratio

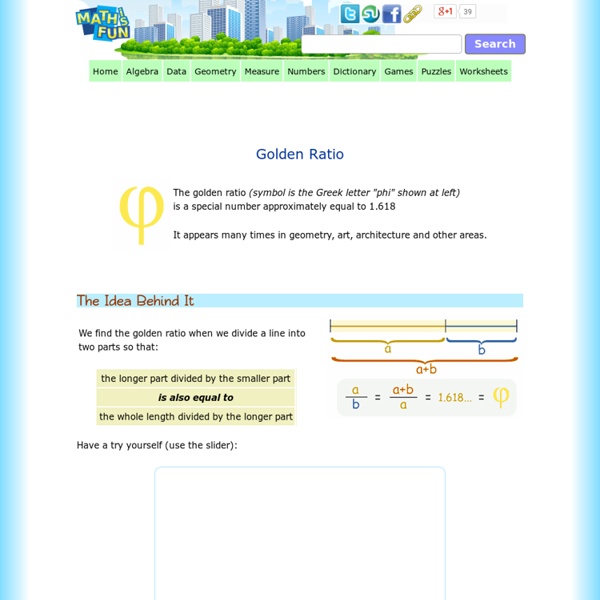
Golden Ratio The golden ratio, also known as the divine proportion, golden mean, or golden section, is a number often encountered when taking the ratios of distances in simple geometric figures such as the pentagon, pentagram, decagon and dodecahedron. It is denoted , or sometimes The designations "phi" (for the golden ratio conjugate ) and "Phi" (for the larger quantity ) are sometimes also used (Knott), although this usage is not necessarily recommended. The term "golden section" (in German, goldener Schnitt or der goldene Schnitt) seems to first have been used by Martin Ohm in the 1835 2nd edition of his textbook Die Reine Elementar-Mathematik (Livio 2002, p. 6). ("phi") was apparently first used by Mark Barr at the beginning of the 20th century in commemoration of the Greek sculptor Phidias (ca. 490-430 BC), who a number of art historians claim made extensive use of the golden ratio in his works (Livio 2002, pp. 5-6). is an abbreviation of the Greek tome, meaning "to cut." giving for the line segment

Sezione aurea di un segmento Sezione aurea di un segmento ( A cura di Nannelli Lorenzo) La sezione aurea di un segmento, per definizione, è la parte del segmento che risulta media proporzionale tra l’intero segmento e la parte dello stesso che rimane sottraendo al segmento la sua parte aurea. Nella figura a lato è indicato il segmento AB ed è indicato il punto P interno ad esso. , affinché il segmento AP sia la parte aurea del segmento AB la misura x (positiva) deve verificare la seguente proporzione Osserviamo che , quindi la sezione aurea di un segmento rappresenta quasi il 62% del segmento. Teorema: il lato del decagono regolare è uguale alla sezione aurea del raggio della circonferenza in cui è inscritto. Dimostrazione Per dimostrare ciò si deve considerare un triangolo isoscele avente l’angolo al vertice di 36° (e conseguentemente i due angoli alla base di misura 72°) e far vedere che la base del triangolo rappresenta la sezione aurea del lato. dalla quale emerge che si può anche scrivere

SEZIONE AUREA prof Giuseppe Spina H o apprezzato molto questo lavoro del prof. Giuseppe Spina docente di matematica - fisica e vicario del Liceo Artistico Statale di Cosenza sul rapporto fra le grandezze con specifica focalizzazione sulla “Sezione aurea del segmento”. gusto nel sapere trasferire agli altri nozioni e concetti, frutto anche della sua ultra trentennale esperienza di docente. ormai pregiudizialmente rifiutano l’autorità costituita così come ogni apprendimento che viene loro imposto. innovative e pressanti di pratiche informatiche sempre più egemonizzanti. potremmo chiosare che il prof. come elemento di equilibrio, in quanto rispetta armoniosamente le proporzioni tra il tradizionale ed il modulare . Si dice sezione aurea di un segmento quella parte del segmento (la maggiore), che è media proporzionale fra l’intero segmento e la rimanente parte ( la minore). Se il punto E divide il segmento AB in due parti tali che si abbia: diremo che AE è la sezione aurea del segmento AB. C e D. sostituendo si ha :

Sezione Aurea - Geometria Ripartizione di un segmento in due parti, che stanno tra loro come la maggiore (a) sta al segmento intero (1); utilizzando i simboli si ha: 1:a=a:b. Se AB è il segmento dato, si conduca la per perpendicolare ad AB nell’estremo B e si prenda su di esso il segmento BO, metà di AB, indi col centro in O si descriva la circonferenza di raggio OB, che risulterà tangente in B alla retta AB. Si unisca A con O e si chiamino C e D le intersezioni della retta AO con la circonferenza; si porti infine su AB il segmento AE congruente ad AC. Infatti per il teorema della secante e della tangente (se da un punto si conducono ad una circonferenza una secante e una tangente, il segmento determinato dalla circonferenza sulla tangente è medio proporzionale fra i segmenti determinati sulla secante e aventi un estremo in quel punto) si ha: Esiste uno speciale rettangolo le cui proporzioni corrispondono alla sezione aurea. e dunque: