


Quantum spacetime In mathematical physics, the concept of quantum spacetime is a generalization of the usual concept of spacetime in which some variables that ordinarily commute are assumed not to commute and form a different Lie algebra. The choice of that algebra still varies from theory to theory. As a result of this change some variables that are usually continuous may become discrete. Often only such discrete variables are called "quantized"; usage varies. Physical reasons have been given to believe that physical spacetime is a quantum spacetime. are already noncommutative, obey the Heisenberg uncertainty principle, and are continuous. Again, physical spacetime is expected to be quantum because physical coordinates are already slightly noncommutative. Both arguments are based on pure gravity and quantum theory, and they limit the measurement of time by the only time constant in pure quantum gravity, the Planck time. The Lie algebra should be semisimple (Yang, I. Bicrossproduct model spacetime[edit]
Coulomb's law Value of the constant[edit] The exact value of Coulomb's constant ke comes from three of the fundamental, invariant quantities that define free space in the SI system: the speed of light c0 , magnetic permeability μ0 , and electric permittivity ε0 , related by Maxwell as: Use of Coulomb's constant[edit] Coulomb's constant is used in many electric equations, although it is sometimes expressed as the following product of the vacuum permittivity constant: Some examples of use of Coulomb's constant are the following: Coulomb's law: Electric potential energy: Electric field: See also[edit] References[edit] DNA molecules can 'teleport', Nobel Prize winner claims A Nobel Prize winning biologist has ignited controversy after publishing details of an experiment in which a fragment of DNA appeared to ‘teleport’ or imprint itself between test tubes. According to a team headed by Luc Montagnier, previously known for his work on HIV and AIDS, two test tubes, one of which contained a tiny piece of bacterial DNA, the other pure water, were surrounded by a weak electromagnetic field of 7Hz. Eighteen hours later, after DNA amplification using a polymerase chain reaction, as if by magic the DNA was detectable in the test tube containing pure water. Oddly, the original DNA sample had to be diluted many times over for the experiment to work, which might explain why the phenomenon has not been detected before, assuming that this is what has happened. The phenomenon might be very loosely described as 'teleportation' except that the bases project or imprint themselves across space rather than simply moving from one place to another. What does all of this mean?
Uncertainty reigns over Heisenberg's measurement analogy A row has broken out among physicists over an analogy used by Werner Heisenberg in 1927 to make sense of his famous uncertainty principle. The analogy was largely forgotten as quantum theory became more sophisticated but has enjoyed a revival over the past decade. While several recent experiments suggest that the analogy is flawed, a team of physicists in the UK, Finland and Germany is now arguing that these experiments are not faithful to Heisenberg's original formulation. Heisenberg's uncertainty principle states that we cannot measure certain pairs of variables for a quantum object – position and momentum, say – both with arbitrary accuracy. When Heisenberg proposed the principle in 1927, he offered a simple physical picture to help it make intuitive sense. Not necessarily wrong Then in 1988 Masanao Ozawa at Nagoya University in Japan argued that Heisenberg's original relationship between error and disturbance does not represent a fundamental limit of uncertainty. Truer to Heisenberg?
Gravitational constant The gravitational constant, approximately 6.67×10−11 N·(m/kg)2 and denoted by letter G, is an empirical physical constant involved in the calculation(s) of gravitational force between two bodies. It usually appears in Sir Isaac Newton's law of universal gravitation, and in Albert Einstein's theory of general relativity. It is also known as the universal gravitational constant, Newton's constant, and colloquially as Big G.[1] It should not be confused with "little g" (g), which is the local gravitational field (equivalent to the free-fall acceleration[2]), especially that at the Earth's surface. Laws and constants[edit] According to the law of universal gravitation, the attractive force (F) between two bodies is directly proportional to the product of their masses (m1 and m2), and inversely proportional to the square of the distance, r, (inverse-square law) between them: The constant of proportionality, G, is the gravitational constant. with relative standard uncertainty 1.2×10−4.[4] . and
Quantum Physics Revealed As Non-Mysterious This is one of several shortened indices into the Quantum Physics Sequence. Hello! You may have been directed to this page because you said something along the lines of "Quantum physics shows that reality doesn't exist apart from our observation of it," or "Science has disproved the idea of an objective reality," or even just "Quantum physics is one of the great mysteries of modern science; no one understands how it works." There was a time, roughly the first half-century after quantum physics was invented, when this was more or less true. The series of posts indexed below will show you - not just tell you - what's really going on down there. Some optional preliminaries you might want to read: Reductionism: We build models of the universe that have many different levels of description. And here's the main sequence: Quantum Explanations: Quantum mechanics doesn't deserve its fearsome reputation.
Quantum entanglement Quantum entanglement is a physical phenomenon that occurs when pairs or groups of particles are generated or interact in ways such that the quantum state of each particle cannot be described independently – instead, a quantum state may be given for the system as a whole. Such phenomena were the subject of a 1935 paper by Albert Einstein, Boris Podolsky and Nathan Rosen,[1] describing what came to be known as the EPR paradox, and several papers by Erwin Schrödinger shortly thereafter.[2][3] Einstein and others considered such behavior to be impossible, as it violated the local realist view of causality (Einstein referred to it as "spooky action at a distance"),[4] and argued that the accepted formulation of quantum mechanics must therefore be incomplete. History[edit] However, they did not coin the word entanglement, nor did they generalize the special properties of the state they considered. Concept[edit] Meaning of entanglement[edit] Apparent paradox[edit] The hidden variables theory[edit]
Boltzmann constant The Boltzmann constant (kB or k), named after Ludwig Boltzmann, is a physical constant relating energy at the individual particle level with temperature. It is the gas constant R divided by the Avogadro constant NA: It has the same dimension (energy divided by temperature) as entropy. The accepted value in SI units is 1.3806488(13)×10−23 J/K. Bridge from macroscopic to microscopic physics[edit] where R is the gas constant (8.314 4621(75) J K−1 mol−1[1]). The left-hand side of the equation is a macroscopic amount of pressure-volume energy representing the state of the bulk gas. Role in the equipartition of energy[edit] Given a thermodynamic system at an absolute temperature T, the thermal energy carried by each microscopic "degree of freedom" in the system is on the order of magnitude of kBT/2 (i. e., about 2.07×10−21 J, or 0.013 eV, at room temperature). Application to simple gas thermodynamics[edit] Kinetic theory gives the average pressure p for an ideal gas as gives History[edit]
NASA to Launch Spacecraft to Keep Track of Global Carbon Dioxide - SciTech Daily NASA is about to launch the Orbiting Carbon Observatory – a satellite dedicated to the study of global carbon dioxide sources that will help researchers predict the future of climate change. In the lexicon of climate change, one word appears more often than any other: “carbon.” Carbon credits, carbon emissions, carbon sequestration…. These terms are on everyone’s lips. The reason is carbon dioxide (CO2). According to the Intergovernmental Panel on Climate Change, CO2 is the most important driver of global warming. NASA is about to launch a spacecraft to keep track of this greenhouse gas. A new ScienceCast video explores the goals and underlying technology of the Orbiting Carbon Observatory. Also known as “OCO-2″, the polar orbiting satellite will provide a global picture of human and natural sources of carbon dioxide. Although the mission is named OCO two, it is actually NASA’s first spacecraft dedicated to measuring atmospheric carbon dioxide levels. It’s coming just in time. Source: Dr.
Efimov state The Efimov effect is an effect in the quantum mechanics of Few-body systems predicted by the Russian theoretical physicist V. N. Efimov[1][2] in 1970. Efimov’s effect refers to a scenario in which three identical bosons interact, with the prediction of an infinite series of excited three-body energy levels when a two-body state is exactly at the dissociation threshold. The unusual Efimov state has an infinite number of similar states. In 2005, for the first time the research group of Rudolf Grimm and Hanns-Christoph Nägerl from the Institute for Experimental Physics (University of Innsbruck, Austria) experimentally confirmed such a state in an ultracold gas of caesium atoms. The interest in the "universal phenomena" of cold atomic gases is still growing, especially because of the long awaited experimental results.[8][9] The discipline of universality in cold atomic gases nearby the Efimov states are sometimes commonly referred to as "Efimov physics". References[edit] Jump up ^ В.И.
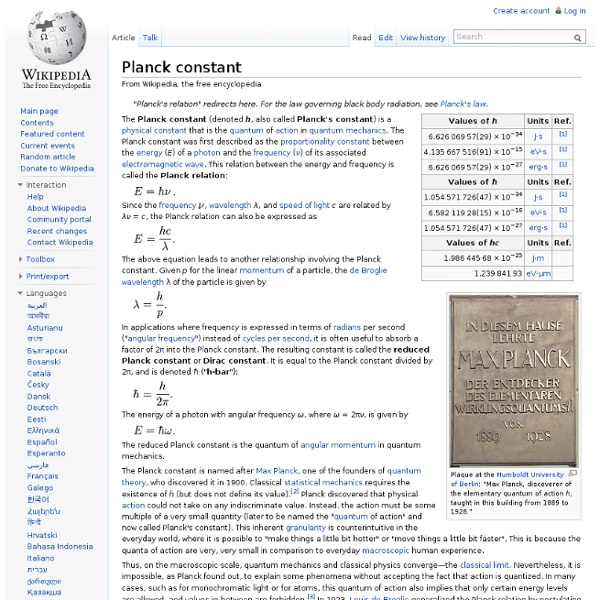
Planck units Originally proposed in 1899 by German physicist Max Planck, these units are also known as natural units because the origin of their definition comes only from properties of the fundamental physical theories and not from interchangeable experimental parameters. Planck units are only one system of natural units among other systems, but are considered unique in that these units are not based on properties of any prototype object or particle (that would be arbitrarily chosen), but rather on properties of free space alone. The universal constants that Planck units, by definition, normalize to 1 are: the gravitational constant, G,the reduced Planck constant, ħ,the speed of light in a vacuum, c,the Coulomb constant, (4πε0)−1 (sometimes ke or k), andthe Boltzmann constant, kB (sometimes k). Planck units are sometimes called "God's units",[1][2] since Planck units are free of anthropocentric arbitrariness. Natural units help physicists to reframe questions. Base units[edit] can be expressed as
New NASA/NOAA Animations Reveal Water Vapor Over Oceans - SciTech Daily The movement of upper-air water vapor over the Eastern Pacific is shown using GOES satellite air temperature data. High, cold clouds are white. High, cold, clear air (around -28 F) is blue. Lower, warmer, dry air (around -10 F) is magenta (where clear, dry air penetrates lower in the atmosphere). Image Credit: NASA/NOAA GOES Project Dennis Chesters Scientists have used observations from the National Oceanic and Atmospheric Administration’s Geostationary Operational Environmental Satellites to create two new types of animations that indicate where water vapor is moving over the Atlantic and Eastern Pacific oceans. Knowing where water vapor is in the atmosphere is one of many factors forecasters use to identify weather features. Observations from the National Oceanic and Atmospheric Administration’s Geostationary Operational Environmental Satellites (GOES) measure the local air temperature in kelvins (degrees Kelvin) at different layers of the atmosphere. Related links
Amplituhedron An amplituhedron is a geometric structure that enables simplified calculation of particle interactions in some quantum field theories. In planar N = 4 supersymmetric Yang–Mills theory, an amplituhedron is defined as a mathematical space known as the positive Grassmannian. The connection between the amplituhedron and scattering amplitudes is at present a conjecture that has passed many non-trivial checks, including an understanding of how locality and unitarity arise as consequences of positivity. Research has been led by Nima Arkani-Hamed. Description[edit] In the approach, the on-shell scattering process "tree" is described by a positive Grassmannian, a structure in algebraic geometry analogous to a convex polytope, that generalizes the idea of a simplex in projective space.[2] A polytope is a kind of higher dimensional polyhedron, and the values being calculated are scattering amplitudes, and so the object is called an amplituhedron.[5] Implications[edit] See also[edit] References[edit]