Why the circle of fourths is so important when learning major scales
Playing your major scales should be a part of your daily practice regimen. However, practicing them in a “circle of fourths” or “circle of fifths” pattern is even better. Let’s focus more on circle of fourths. If you type “circle of fourths” or “circle of fifths” in google, you can actually find a host of other examples.
Egyptian Fractions
1 Egyptian Fractions The ancient Egyptians only used fractions of the form 1/n so any other fraction had to be represented as a sum of such unit fractions and, furthermore, all the unit fractions were different! Why? Is this a better system than our present day one? In fact, it is for some tasks. This page explores some of the history and methods with puzzles and and gives you a summary of computer searches for such representations.
Harmonic series (music)
Harmonic series of a string with terms written as reciprocals (2/1 written as 1/2). A harmonic series is the sequence of all multiples of a base frequency. Any complex tone "can be described as a combination of many simple periodic waves (i.e., sine waves) or partials, each with its own frequency of vibration, amplitude, and phase."[1] (Fourier analysis) A partial is any of the sine waves by which a complex tone is described.
Where Math meets Music
Where Math meets Music Ever wonder why some note combinations sound pleasing to our ears, while others make us cringe? To understand the answer to this question, you’ll first need to understand the wave patterns created by a musical instrument.
Circle of fifths
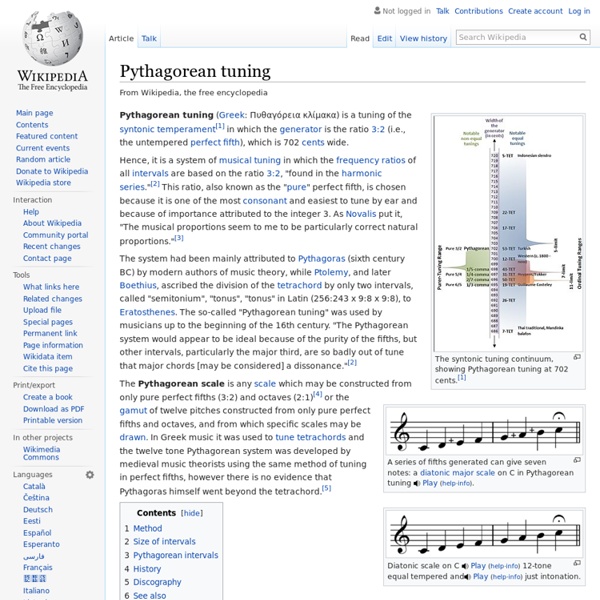
Circle of fifths showing major and minor keys Nikolay Diletsky's circle of fifths in Idea grammatiki musikiyskoy (Moscow, 1679) In music theory, the circle of fifths (or circle of fourths) is a visual representation of the relationships among the 12 tones of the chromatic scale, their corresponding key signatures, and the associated major and minor keys. More specifically, it is a geometrical representation of relationships among the 12 pitch classes of the chromatic scale in pitch class space. Definition[edit] Structure and use[edit]
LucyTuning*LucyScaleDevelopments*Pi tuning*LucyTuned Lullabies*John "Longitude" Harrison
Setting tuning and harmonic standards into the future. Have fun with them. LucyTuned Lullabies (from around the world) New LucyTune site (May 2005) BBC Radio 4 interview with Robert Sandall about LucyTuning mp3 - (3min 54 seconds) LucyTuning - musical tuning, harmonic, composition, practice, specifications, and theory
5 Ways to Use Non-Diatonic Notes in Jazz Improvisation
You want to play exciting solos… Ones that will make the audience sit on the edge of their seats, that’ll make you stand out from every other musician in the room. …except when you improvise everything ends up sounding exactly the same. Many musicians share this frustration and for many it goes right back to the standard approach to improvisation that you find in most books. The mentality that each chord has a designated scale: Major scales for major chordsDorian for minor chordsMixolydian for V7 chords
Here’s Why You Should Convert Your Music To 432 Hz
“If you want to find the secrets of the universe, think in terms of energy, frequency and vibration.” – Nikola Tesla“What we have called matter is energy, whose vibration has been so lowered as to be perceptible to the senses. There is no matter.” – Albert Einstein Tesla said it. Einstein Agreed. Science proved it. It is a known fact that everything—including our own bodies—is made up of energy vibrating at different frequencies.