

Laplace transform. History[edit] The Laplace transform is named after mathematician and astronomer Pierre-Simon Laplace, who used a similar transform (now called z transform) in his work on probability theory.
The current widespread use of the transform came about soon after World War II although it had been used in the 19th century by Abel, Lerch, Heaviside, and Bromwich. From 1744, Leonhard Euler investigated integrals of the form as solutions of differential equations but did not pursue the matter very far.[2] Joseph Louis Lagrange was an admirer of Euler and, in his work on integrating probability density functions, investigated expressions of the form which some modern historians have interpreted within modern Laplace transform theory.[3][4][clarification needed] akin to a Mellin transform, to transform the whole of a difference equation, in order to look for solutions of the transformed equation.
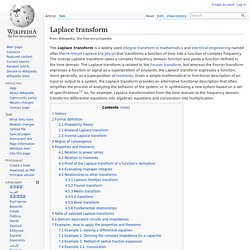
Formal definition[edit] The parameter s is the complex number frequency: with real numbers and ω. instead of F. State-space representation. In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations.
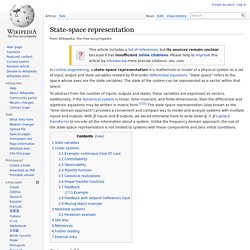
"State space" refers to the space whose axes are the state variables. The state of the system can be represented as a vector within that space. To abstract from the number of inputs, outputs and states, these variables are expressed as vectors. Additionally, if the dynamical system is linear, time-invariant, and finite-dimensional, then the differential and algebraic equations may be written in matrix form.[1][2] The state-space representation (also known as the "time-domain approach") provides a convenient and compact way to model and analyze systems with multiple inputs and outputs. With. Feedback. "...'feedback' exists between two parts when each affects the other.
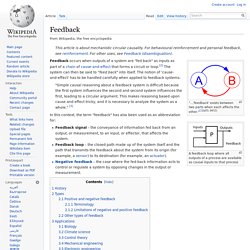
"[1](p53, §4/11) A feedback loop where all outputs of a process are available as causal inputs to that process. Dynamical system. The Lorenz attractor arises in the study of the Lorenz Oscillator, a dynamical system.
Overview[edit] Before the advent of computers, finding an orbit required sophisticated mathematical techniques and could be accomplished only for a small class of dynamical systems. Numerical methods implemented on electronic computing machines have simplified the task of determining the orbits of a dynamical system. For simple dynamical systems, knowing the trajectory is often sufficient, but most dynamical systems are too complicated to be understood in terms of individual trajectories. The difficulties arise because: The systems studied may only be known approximately—the parameters of the system may not be known precisely or terms may be missing from the equations.
History[edit] Many people regard Henri Poincaré as the founder of dynamical systems.[3] Poincaré published two now classical monographs, "New Methods of Celestial Mechanics" (1892–1899) and "Lectures on Celestial Mechanics" (1905–1910). . THE GENERAL SYSTEM? REVIEWED by Charles Francois, Editor, International Encyclopedia of Cybernetics and Systemics By Thomas Mandel "A human being is part of the Whole...He experiences himself, his thoughts and feelings, as something separated from the rest...a kind of optical delusion of his consciousness.

This delusion is a kind of prison for us, restricting us to our personal desires and to affection for a few persons nearest us. Our task must be to free ourselves from this prison by widening our circle of compassion to embrace all living creatures and the whole of nature in its beauty. Introduction to Principia Cybernetica. Systems Thinking, Systems Tools and Chaos Theory. © Copyright Carter McNamara, MBA, PhD, Authenticity Consulting, LLC.

Adapted from the Field Guide to Consulting and Organizational Development and Field Guide to Consulting and Organizational Development with Nonprofits. Three of the biggest breakthroughs in how we understand and successfully guide changes in ourselves, others and organizations are systems theory, systems thinking and systems tools. To understand how they are used, we first must understand the concept of a system. Many of us have an intuitive understanding of the concept. However, we need to make that intuition even more explicit in order to use systems thinking and systems tools. Sections of This Topic Include Basics -- Definitions - - - What's a System? Also seeRelated Library Topics.
Conceptual model. A conceptual model is a model made of the composition of concepts, which are used to help people know, understand, or simulate a subject the model represents.
Some models are physical objects; for example, a toy model which may be assembled, and may be made to work like the object it represents. The term conceptual model may be used to refer to models which are formed after a conceptualization (generalization)[1] process in the mind. Conceptual models represent human intentions or semantics[citation needed][dubious ]. Conceptualization from observation of physical existence and conceptual modeling are the necessary means that humans employ to think and solve problems[citation needed].
Concepts are used to convey semantics during natural language based communication[citation needed]. Systems engineering. Systems engineering techniques are used in complex projects: spacecraft design, computer chip design, robotics, software integration, and bridge building.
Systems engineering uses a host of tools that include modeling and simulation, requirements analysis and scheduling to manage complexity. Systems engineering is an interdisciplinary field of engineering that focuses on how to design and manage complex engineering systems over their life cycles. Homeostasis. Homeostasis, also spelled homoeostasis (from Greek: ὅμοιος homœos, "similar" and στάσις stasis, "standing still"), is the property of a system in which variables are regulated so that internal conditions remain stable and relatively constant.
Examples of homeostasis include the regulation of temperature and the balance between acidity and alkalinity (pH). It is a process that maintains the stability of the human body's internal environment in response to changes in external conditions. The concept was described by French physiologist Claude Bernard in 1865 and the word was coined by Walter Bradford Cannon in 1926.[1] Although the term was originally used to refer to processes within living organisms, it is frequently applied to automatic control systems such as thermostats.
Homeostasis requires a sensor to detect changes in the condition to be regulated, an effector mechanism that can vary that condition; and a negative feedback connection between the two. Biological[edit] System dynamics. Dynamic stock and flow diagram of model New product adoption (model from article by John Sterman 2001) System dynamics is an approach to understanding the behaviour of complex systems over time.
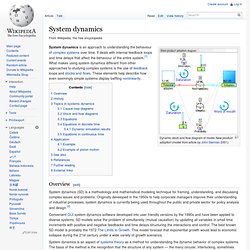
It deals with internal feedback loops and time delays that affect the behaviour of the entire system.[1] What makes using system dynamics different from other approaches to studying complex systems is the use of feedback loops and stocks and flows. These elements help describe how even seemingly simple systems display baffling nonlinearity. Overview[edit] Systems theory. What is Systems Theory? Systems theory is an interdisciplinary theory about the nature of complex systems in nature, society, and science, and is a framework by which one can investigate and/or describe any group of objects that work together to produce some result.
This could be a single organism, any organization or society, or any electro-mechanical or informational artifact. As a technical and general academic area of study it predominantly refers to the science of systems that resulted from Bertalanffy's General System Theory (GST), among others, in initiating what became a project of systems research and practice. Systems theoretical approaches were later appropriated in other fields, such as in the structural functionalist sociology of Talcott Parsons and Niklas Luhmann. Overview Margaret Mead was an influential figure in systems theory. Contemporary ideas from systems theory have grown with diversified areas, exemplified by the work of Béla H.
A system from this Russell Ackoff, Béla H. History. Calculus. History[edit] Modern calculus was developed in 17th century Europe by Isaac Newton and Gottfried Wilhelm Leibniz (see the Leibniz–Newton calculus controversy), but elements of it have appeared in ancient Greece, China, medieval Europe, India, and the Middle East. Ancient[edit] The ancient period introduced some of the ideas that led to integral calculus, but does not seem to have developed these ideas in a rigorous and systematic way. Medieval[edit]