

SS - Angle Side Side. What about SSA (Side Side Angle) theorem?
There is NO SUCH THING!!!! The ASS Postulate does not exist because an angle and two sides does not guarantee that two triangles are congruent. If two triangles have two congruent sides and a congruent non included angle, then triangles are NOT NECESSARILLY congruent. SS - Bisecting Angles (animated) SS - Bisecting Angles with Compass. SS - Congruent Triangles. Definition: Triangles are congruent when all corresponding sides and interior angles are congruent.
The triangles will have the same shape and size, but one may be a mirror image of the other. In the simple case below, the two triangles PQR and LMN are congruent because every corresponding side has the same length, and every corresponding angle has the same measure. The angle at P has the same measure (in degrees) as the angle at L, the side PQ is the same length as the side LM etc. Try this Drag any orange dot at P,Q,R. The other triangle LMN will change to remain congruent to it. In the diagram above, the triangles are drawn next to each other and it is obvious they are identical. Imagine the triangles are cardboard One way to think about triangle congruence is to imagine they are made of cardboard. SS - Circle through 3 points. Drawing a circle through three given points with compass and straightedge 1.

Draw the only circle that passes through the three points below. 2. SS - Classification of Quadrilaterals. SS - Compass and Parallel Lines. SS - Congruent Triangles. Congruent triangles are a special type of similar triangles.

Congruent triangles have the same shape (similar triangles) and size. Increase/decrease <A, <B and <C by clicking and dragging the vertices of the left triangle below. Notice the corresponding angles (<D <E and <F) remain congruent. Since the sum of three angles must be 180o, the third pair of corresponding angles must also be congruent when the first two pairs of corresponding angles are congruent. SS - Congruent Triangles. SS - Constructions. Introduction to constructions Constructions: The drawing of various shapes using only a pair of compasses and straightedge or ruler.
No measurement of lengths or angles is allowed. The word construction in geometry has a very specific meaning: the drawing of geometric items such as lines and circles using only compasses and straightedge or ruler. Very importantly, you are not allowed to measure angles with a protractor, or measure lengths with a ruler. Compasses Compasses are a drawing instrument used for drawing circles and arcs. This kind of compass has nothing to do with the kind used find the north direction when you are lost. SS - Geometry 2007. Sign In | My Account | HMHEducation | eServices | Online Store | Contact Us | FAQ Find another book Search: Geometry, 2007.
SS - Geometry Rotations Explained (90, 180, 270, 360) SS - Net of a Cone and a Cylinder. SS - Platonic Realms Home Page. Sally Simplewit's mother has been rearranging the dining room again, but she is frustrated; the place she wants to put the dining room table isn't working out, because the floor there is smooth but uneven, and she can't seem to get the table into a position where it doesn't rock.

It is a round table, with four legs of equal length. Frustrated, she announces that she is going to get a saw and shorten one of the table's legs. Sally, who has been watching the proceedings with some amusement, tells her mother to relax, and to put the saw away. "For," says Sally, "I guarantee I can get all four legs firmly on the floor without changing either the floor or the lengths of the legs! " Today's challenge: How can Sally make such a guarantee? Solution to yesterday's challenge THE MATH STORE LIVES! NEW FOR 2012: Platonic Realms is at last being rewritten and moved to a new server. This site is registered with the Internet Content Rating Association (ICRA), and is suitable for all ages. SS - Quadrilateral Hierarchy. SS - Rotational Symmetry. Maths Rotational Symmetry Symmetry means balance or form.

In maths we often talk about shapes and things being symmetrical. There are two types of symmetry, line symmetry and rotational symmetry. We have already covered line symmetry. SS - Rotational Symmetry. The rotational symmetry of a shape explains that when an object is rotated on its own axis, the shape of the object looks the same.
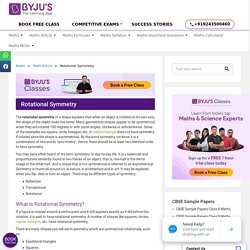
Many geometrical shapes appear to be symmetrical when they are rotated 180 degrees or with some angles, clockwise or anticlockwise. Some of the examples are square, circle, hexagon, etc. A scalene triangle does not have symmetry if rotated since the shape is asymmetrical. By the word symmetry, we know it is a combination of two words ‘sync+metry’. Hence, there should be at least two identical order to have symmetry.
You may have often heard of the term ‘symmetry’ in day-to-day life. ReflectionTranslationalRotational. SS - Similar Triangles. Definition: Triangles are similar if they have the same shape, but can be different sizes.
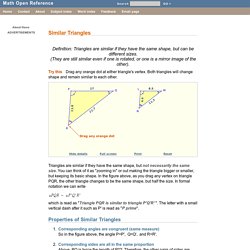
(They are still similar even if one is rotated, or one is a mirror image of the other). Try this Drag any orange dot at either triangle's vertex. Both triangles will change shape and remain similar to each other. SS - Similar Triangles Applications. Image Source: A powerful Zoom lens for a 35mm camera can be very expensive, because it actually contains a number of highly precise glass lenses, which need to be moved by a tiny motor into very exact positions as the camera auto focuses. The Geometry and Mathematics of these lenses is very involved, and they cannot be simply mass produced and tested by computer robots. Lots of effort required to manufacture these lenses results in their very high price tags. Here is a diagram showing how the zoom lens internal arrangement changes as we zoom from 18mmm wide angle to 200mm fully zoomed in: Image Source: Image Copyright 2013 by Passy’s World of Mathematics Shown above are some band photographs taken by Passy with a special low light camera.
Unfortunately this camera does not have a zoom lens, and so you need to be right up close to the stage to take good pictures. A special low light aperture 1.4 zoom lens for taking band photographs has a price tag a bit out of Passy’s current reach. Subscribe. SS - Similar Triangles Definitions and Problems. Definition Generally, two triangles are said to be similar if they have the same shape, even if they are scaled, rotated or even flipped over. SS - Some Coordinates in Rotation. SS - Tessellations. SS - Tessellation. A pattern of shapes that fit perfectly together! A Tessellation (or Tiling) is when we cover a surface with a pattern of flat shapes so that there are no overlaps or gaps. Examples: Rectangles Octagons and Squares Different Pentagons Regular Tessellations. SS - Transformations Review. SS - Transformation Rules Sheet. SS - Word Problems. SS - World's Hardest Easy Geometry Problem.
StudyJams. Virtual Nerd.