

Ricci flow. Several stages of Ricci flow on a 2D manifold.

In differential geometry, the Ricci flow (/ˈriːtʃi/) is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric. Mathematical definition[edit] Given a Riemannian manifold with metric tensor , we can compute the Ricci tensor The normalized Ricci flow makes sense for compact manifolds and is given by the equation where.
Differentiable manifold. A nondifferentiable atlas of charts for the globe.

The results of calculus may not be compatible between charts if the atlas is not differentiable. Category:Curves. Holonomy. Parallel transport on a sphere depends on the path.
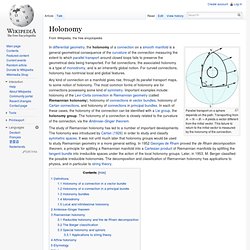
Transporting from A → N → B → A yields a vector different from the initial vector. This failure to return to the initial vector is measured by the holonomy of the connection. The study of Riemannian holonomy has led to a number of important developments. The holonomy was introduced by Cartan (1926) in order to study and classify symmetric spaces. It was not until much later that holonomy groups would be used to study Riemannian geometry in a more general setting. Definitions[edit] Supersingular K3 surface. Conjectures[edit] More generally, a smooth projective variety X over a field of characteristic p > 0 is called supersingular if all slopes of Frobenius on the crystalline cohomology Ha(X,W(k)) are equal to a/2, for all a.
In particular, this gives the standard notion of a supersingular abelian variety. For a variety X over a finite field Fq, it is equivalent to say that the eigenvalues of Frobenius on the l-adic cohomology Ha(X,Ql) are equal to qa/2 times roots of unity. It follows that any variety in positive characteristic whose l-adic cohomology is generated by algebraic cycles is supersingular.
A K3 surface whose l-adic cohomology is generated by algebraic cycles is sometimes called a Shioda supersingular K3 surface. Conversely, the Tate conjecture would imply that every supersingular K3 surface over an algebraically closed field has Picard number 22. Monodromy. Definition[edit] Let X be a connected and locally connected based topological space with base point x, and let .
For a loop γ: [0, 1] → X based at x, denote a lift under the covering map (starting at a point ) by . Morse theory. "Morse function" redirects here.
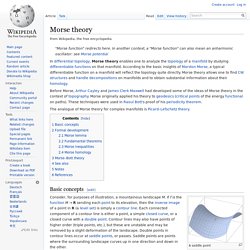
In another context, a "Morse function" can also mean an anharmonic oscillator: see Morse potential The analogue of Morse theory for complex manifolds is Picard–Lefschetz theory. Basic concepts[edit] Contour lines around a saddle point To each of these three types of critical points – basins, passes, and peaks (also called minima, saddles, and maxima) – one associates a number called the index. Define Ma as f−1(−∞, a]. These figures are homotopy equivalent. One therefore appears to have the following rule: the topology of Mα does not change except when α passes the height of a critical point, and when α passes the height of a critical point of index γ, a γ-cell is attached to Mα. This rule, however, is false as stated.
Formal development[edit] For the functions from R to R, f has a critical point at the origin if b=0, which is non-degenerate if c≠0 (i.e. f is of the form a+cx2+...) and degenerate if c=0 (i.e. f is of the form a+dx3+...). Morse lemma[edit] . K3 surface. Dans la seconde partie de mon rapport, il s'agit des variétés kählériennes dites K3, ainsi nommées en l'honneur de Kummer, Kähler, Kodaira et de la belle montagne K2 au Cachemire André Weil (1958, p.546), describing the reason for the name "K3 surface" In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.
In the Enriques–Kodaira classification of surfaces they form one of the 4 classes of surfaces of Kodaira dimension 0. Together with two-dimensional complex tori, they are the Calabi–Yau manifolds of dimension two. Most complex K3 surfaces are not algebraic. Vector bundle. In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X.
The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x) = V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X × V over X. Such vector bundles are said to be trivial. Vector bundles are almost always required to be locally trivial, however, which means they are examples of fiber bundles. Definition and first consequences[edit] Riemannian geometry. Elliptic geometry is also sometimes called "Riemannian geometry".

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area, and volume. From those some other global quantities can be derived by integrating local contributions. Differential geometry of surfaces. In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric.
Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. Riemannian manifold. In differential geometry, a (smooth) Riemannian manifold or (smooth) Riemannian space (M,g) is a real smooth manifold M equipped with an inner product on the tangent space at each point that varies smoothly from point to point in the sense that if X and Y are vector fields on M, then.
Orbifold. Differential topology. In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds. Description[edit] On the other hand, smooth manifolds are more rigid than the topological manifolds. John Milnor discovered that some spheres have more than one smooth structure—see exotic sphere and Donaldson's theorem.
Kervaire exhibited topological manifolds with no smooth structure at all.[1] Some constructions of smooth manifold theory, such as the existence of tangent bundles,[2] can be done in the topological setting with much more work, and others cannot. Special unitary group. The SU(n) groups find wide application in the Standard Model of particle physics, especially SU(2) in the electroweak interaction and SU(3) in QCD.[1] Properties[edit] The special unitary group SU(n) is a real Lie group (though not a complex Lie group).
Its dimension as a real manifold is n2 − 1. Topologically, it is compact and simply connected. Klein geometry. In mathematics, a Klein geometry is a type of geometry motivated by Felix Klein in his influential Erlangen program. More specifically, it is a homogeneous space X together with a transitive action on X by a Lie group G, which acts as the symmetry group of the geometry. For background and motivation see the article on the Erlangen program.