

Stochastic geometry. In mathematics, stochastic geometry is the study of random spatial patterns.
At the heart of the subject lies the study of random point patterns. This leads to the theory of spatial point processes, hence notions of Palm conditioning, which extend to the more abstract setting of random measures. Models[edit] There are various models for point processes, typically based on but going beyond the classic homogeneous Poisson point process (the basic model for complete spatial randomness) to find expressive models which allow effective statistical methods. Random object[edit] Geometry in Action. This page collects various areas in which ideas from discrete and computational geometry (meaning mainly low-dimensional Euclidean geometry) meet some real world applications.

It contains brief descriptions of those applications and the geometric questions arising from them, as well as pointers to web pages on the applications themselves and on their geometric connections. This is largely organized by application but some major general techniques are also listed as topics. Suggestions for other applications and pointers are welcome. Geometric references and techniques Design and manufacturing Graphics and visualization Information systems Medicine and biology Physical sciences Robotics. The Geometry Junkyard.
Hyperboloid. In mathematics, a hyperboloid is a quadric – a type of surface in three dimensions – described by the equation (hyperboloid of one sheet), or (hyperboloid of two sheets).
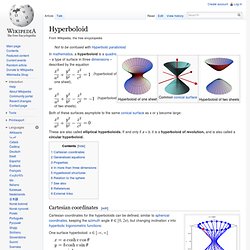
Both of these surfaces asymptote to the same conical surface as x or y become large: These are also called elliptical hyperboloids. Paraboloid. Paraboloid of revolution In mathematics, a paraboloid is a quadric surface of special kind.
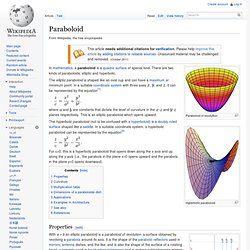
There are two kinds of paraboloids: elliptic and hyperbolic. The elliptic paraboloid is shaped like an oval cup and can have a maximum or minimum point. Hyperbolic geometry. Lines through a given point P and asymptotic to line R.
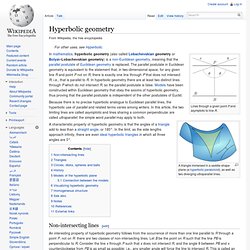
A triangle immersed in a saddle-shape plane (a hyperbolic paraboloid), as well as two diverging ultraparallel lines. In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced. The parallel postulate in Euclidean geometry is equivalent to the statement that, in two-dimensional space, for any given line R and point P not on R, there is exactly one line through P that does not intersect R; i.e., that is parallel to R.
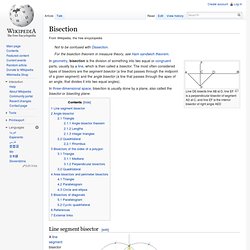
Bisection. Line DE bisects line AB at D, line EF is a perpendicular bisector of segment AD at C, and line EF is the interior bisector of right angle AED.
Dihedral group. Notation[edit] There are two competing notations for the dihedral group associated to a polygon with n sides.
In geometry the group is denoted Dn, while in algebra the same group is denoted by D2n to indicate the number of elements. Coxeter notation is another notation, denoting the reflectional dihedral symmetry as [n], order 2n, and rotational dihedral symmetry as [n]+, order n. Orbifold notation gives the reflective symmetry as *n• and rotational symmetry as n•. In this article, Dn (and sometimes Dihn) refers to the symmetries of a regular polygon with n sides. Orthogonal group. Where QT is the transpose of Q and I is the identity matrix.
This article mainly discusses the orthogonal groups of quadratic forms that may be expressed over some bases as the dot product; over the reals, they are the positive definite quadratic forms. Over the reals, for any non-degenerate quadratic form, there is a basis, on which the matrix of the form is a diagonal matrix such that the diagonal entries are either 1 or −1. Uniform tilings in hyperbolic plane. Uniform tilings can be identified by their vertex configuration, a sequence of numbers representing the number of sides of the polygons around each vertex.
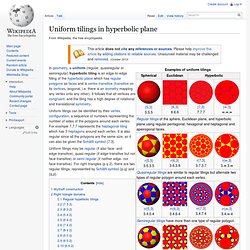
For example 7.7.7 represents the heptagonal tiling which has 3 heptagons around each vertex. It is also regular since all the polygons are the same size, so it can also be given the Schläfli symbol {7,3}. Uniform tilings may be regular (if also face- and edge-transitive), quasi-regular (if edge-transitive but not face-transitive) or semi-regular (if neither edge- nor face-transitive). For right triangles (p q 2), there are two regular tilings, represented by Schläfli symbol {p,q} and {q,p}. Wythoff construction[edit] Example Wythoff construction with right triangles (r=2) and the 7 generator points.
Families with r=2 contain regular hyperbolic tilings, defined by a Coxeter group such as [7,3], [8,3], [9,3], ... [5,4], [6,4], .... More symmetry families can be constructed from fundamental domains that are not triangles. Analytic geometry. Cartesian coordinates Analytic geometry, or analytical geometry, has two different meanings in mathematics.
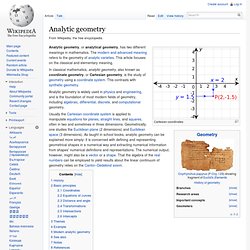
The modern and advanced meaning refers to the geometry of analytic varieties. This article focuses on the classical and elementary meaning. Curvilinear coordinates. Curvilinear, affine, and Cartesian coordinates in two-dimensional space. Euler's rotation theorem. A rotation represented by an Euler axis and angle. The theorem is named after Leonhard Euler, who proved it in 1775 by an elementary geometric argument.
The axis of rotation is known as an Euler axis, typically represented by a unit vector . Knot theory. A knot diagram of the trefoil knot Knots can be described in various ways. Given a method of description, however, there may be more than one description that represents the same knot. Hypercube. An n-dimensional hypercube is also called an n-cube or an n-dimensional cube. The term "measure polytope" is also used, notably in the work of H.S.M. Coxeter (originally from Elte, 1912[1]), but it has now been superseded.
Hypergeometric function. In mathematics, the Gaussian or ordinary hypergeometric function 2F1(a,b;c;z) is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. [It] is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation.
For systematic lists of some of the many thousands of published identities involving the hypergeometric function, see the reference works by Arthur Erdélyi, Wilhelm Magnus, and Fritz Oberhettinger et al. (1953), Abramowitz & Stegun (1965), and Daalhuis (2010).