

Euclid, Elements, BOOK I., BOOK I. PROPOSITIONS., Proposition 1. Euclides Euclid Euklides Euklid - Los Elementos de Euclides - Els Elements d´Euclides - Euklides Elementuak - Euclid´s Elements. Pythagoras in 2 minutes 2. Demostración del teorema de Pitágoras. Euclid. Egyptian Maths. ANCIENT MATH of ETHIOPIA - Amazing Methods of Calculation.flv. NCEA Maths Level 1 Geometric Reasoning: Angles Within Circles. NCEA Maths Level 1 Geometric Reasoning: Angles Within Circles. Shop Math: How to Find the Center of Anything. How to Find the Center of a Circle - Method 2. How To Find The Center Of A Circle - Method 1. How to Find the Center of a Circle. All the possible polygons! All the possible polygons! Basic Construction of Regular polygon. A PERFECT Nonagon with Compass and Straight Edge? Euclid’s Elements: Book 1, Proposition 1. Roger Penrose - Forbidden crystal symmetry in mathematics and architecture. Kepler–Bouwkamp constant.
A sequence of inscribed polygons and circles.
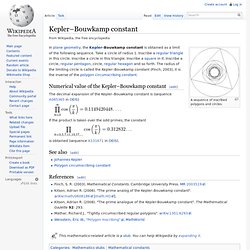
Numerical value of the Kepler–Bouwkamp constant[edit] The decimal expansion of the Kepler–Bouwkamp constant is (sequence A085365 in OEIS) If the product is taken over the odd primes, the constant is obtained (sequence A131671 in OEIS). See also[edit] References[edit] Kepler Mars retrograde - Johannes Kepler. Louration - David Bailey's World of Escher-like Tessellations. Of interest mathematically is that of the colouration possibilities of the tiles.
Here I examine both colouration per se, as an abstract entity (albeit with minimal reference to the in situ tiles for general interest) followed by the in situ pavings, again as a distinct entity. Regarding the coloration as an abstract entity per se, I investigate two aspects. Johannes Kepler - David Bailey's World of Escher-like Tessellations. Johannes Kepler (1571-1630), who although is perhaps better known for his work in astronomy, most notably with his three laws of planetary motion, was also very much concerned with tessellations and polyhedra, and indeed, his interest in the latter very much influenced his astronomical thinking, discussed in more detail below, albeit his ideas were based upon a false premise.
(Incidentally, Kepler has recently been in the news with two contemporary astronomical events. Firstly, in 2004 (and soon again, in June 2012, with a transit of Venus across the Sun of 8 June, as he was the first astronomer to undertake this most difficult task of calculating and then predicting when this occurrence would then take place, the first such determination being of the year 1631. Cruelly, Kepler was denied seeing this, as he died the previous year.
Historical Implication Archimedean Tessellations Star Polygon Tessellations. Pi greco. The Shape of the Great Pyramid - Roger Herz-Fischler - Google Libri. Kepler problem. In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them.
The force may be either attractive or repulsive. The "problem" to be solved is to find the position or speed of the two bodies over time given their masses and initial positions and velocities. Using classical mechanics, the solution can be expressed as a Kepler orbit using six orbital elements. Johannes Kepler's Polyhedra. Johannes Kepler (1571-1630), best known for his three laws of planetary motion, was one of the most outstanding mathematicians of his day.

In addition to his astronomical accomplishments, he systematized and extended all that was known about polyhedra in his time. While previous artist/geometers discovered particular polyhedra, he took a more mathematical approach: he defined classes of polyhedra, discovered the members of the class, and proved that his set was complete. For example, Kepler discovered the infinite class of antiprisms.
In, Harmonice Mundi, Kepler also defined the class of convex uniform polyhedra which we call the Archimedean solids, unfamiliar with the fact that Archimedes had defined the class already. All of these polyhedra except one (the snub dodecahedron, number 13 at the bottom right below) had already appeared in the work of various Renaissance artists. Johannes Kepler's Polyhedra. Sacred Geometry: Flower of Life.
Sacred Geometry - Flower of Life By Andrew Monkman I believe the complete ancient flower of life is an inter-dimensional tool, a portal, a stargate, a window into what some call the inter space plains.
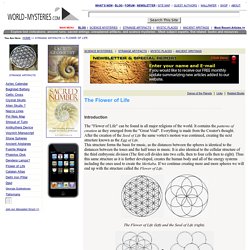
The original flower of life (found on several pillars within "the Osireion" at abydos in Egypt) is incomplete, because it is only the first layer of three (pic1+2). 1. Kepler triangle. A Kepler triangle is a right triangle formed by three squares with areas in geometric progression according to the golden ratio.
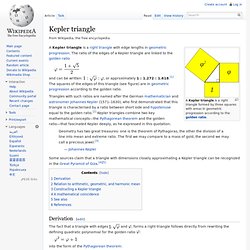
A Kepler triangle is a right triangle with edge lengths in geometric progression. Cerc. Elemente geometrice ale unui cerc: centrul este mov, raza roşie, diametrul albastru, iar circumferinţa neagră.
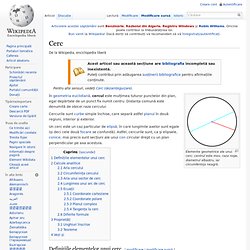
În geometria euclidiană, cercul este mulțimea tuturor punctelor din plan, egal depărtate de un punct fix numit centru. Distanța comună este denumită de obicei raza cercului. Un cerc este un caz particular de elipsă, în care lungimile axelor sunt egale (și deci cele două focare se confundă). Aria cercului. Byrne's edition of Euclid. [ Main Euclid page ] Oliver Byrne's edition of Euclid An unusual and attractive edition of Euclid was published in 1847 in England, edited by an otherwise unknown mathematician named Oliver Byrne.

It covers the first 6 books of Euclid's Elements of Geometry, which range through most of elementary plane geometry and the theory of proportions. What distinguishes Byrne's edition is that he attempts to present Euclid's proofs in terms of pictures, using as little text - and in particular as few labels - as possible. What makes the book especially striking is his use of colour. Category:Elements of Euclid (manuscript from Lüneburg)
Euclide. Da Wikipedia, l'enciclopedia libera.
Euclide Euclide (in greco antico Εὐκλείδης, traslitterato in Euklèides; 323 a.C. – 286 a.C.) è stato un matematico e scienziato greco antico, che visse molto probabilmente durante il regno di Tolomeo I (367 a.C. ca. - 283 a.C.). È stato sicuramente il più importante matematico della storia antica, e uno dei più importanti e riconosciuti di ogni tempo e luogo. Particolarmente significativa è la circostanza che lo accosta a Tolomeo I, perché ci induce a collocarne l'attività principale all'inizio del III secolo a.C. e ci fa supporre che Tolomeo lo abbia chiamato ad operare nella Biblioteca di Alessandria e nell'annesso Museo.
Controversa è invece la notizia secondo cui sarebbe stato un platonico convinto. Euclid biography. Born: about 325 BC Died: about 265 BC in Alexandria, Egypt Click the picture aboveto see six larger pictures Not much younger than these [pupils of Plato] is Euclid, who put together the "Elements", arranging in order many of Eudoxus's theorems, perfecting many of Theaetetus's, and also bringing to irrefutable demonstration the things which had been only loosely proved by his predecessors. This man lived in the time of the first Ptolemy; for Archimedes, who followed closely upon the first Ptolemy makes mention of Euclid, and further they say that Ptolemy once asked him if there were a shorted way to study geometry than the Elements, to which he replied that there was no royal road to geometry. He is therefore younger than Plato's circle, but older than Eratosthenes and Archimedes; for these were contemporaries, as Eratosthenes somewhere says.
There is other information about Euclid given by certain authors but it is not thought to be reliable. .... Euclid's Elements, Introduction. Euclid’s Elements form one of the most beautiful and influential works of science in the history of humankind. Its beauty lies in its logical development of geometry and other branches of mathematics. It has influenced all branches of science but none so much as mathematics and the exact sciences. Assiomi di Hilbert. John Dee’s Mathematical Preface to Euclid. Scuola pitagorica. Da Wikipedia, l'enciclopedia libera. La scuola pitagorica, appartenente al periodo presocratico, fu fondata da Pitagora a Crotone intorno al 530 a.C., sull'esempio delle comunità orfiche e delle sette religiose d'Egitto e di Babilonia, terre che, secondo la tradizione, egli avrebbe conosciuto in occasione dei suoi precedenti viaggi di studio.
La scuola di Crotone ereditò dal suo fondatore la dimensione misterica ma anche l'interesse per la matematica, l'astronomia, la musica e la filosofia. Setta mistica, scientifica, aristocratica[modifica | modifica sorgente] L'originalità della scuola consisteva nel presentarsi come setta mistica-religiosa, comunità scientifica ed insieme partito politico aristocratico che sotto questa veste governò direttamente in alcune città dell'Italia meridionale. Moneta romana raffigurante Pitagora La scuola, che poteva essere frequentata anche dalle donne[3], offriva due tipi di lezione: una pubblica e una privata. GeoGebra. From Wolfram MathWorld. A polygonal number is a type of figurate number that is a generalization of triangular, square, etc., to an -gon for an arbitrary positive integer.
The above diagrams graphically illustrate the process by which the polygonal numbers are built up. Starting with the th triangular number. Numero poligonale.