Using a Protractor. Geoboard - Area and Perimeter. What Is Similarity? Scale drawings. Before studying this lesson about scale drawings,you should review solving proportions Since it is not always possible to draw on paper the actual size of real-life objects such as the real size of a car, an airplane, we need scale drawings to represent the size like the one you see below of a van.
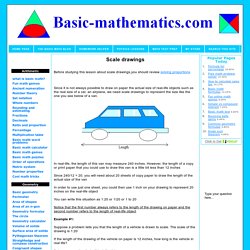
In real-life, the length of this van may measure 240 inches. However, the length of a copy or print paper that you could use to draw this van is a little bit less than 12 inches Since 240/12 = 20, you will need about 20 sheets of copy paper to draw the length of the actual size of the van In order to use just one sheet, you could then use 1 inch on your drawing to represent 20 inches on the real-life object You can write this situation as 1:20 or 1/20 or 1 to 20 Notice that the first number always refers to the length of the drawing on paper and the second number refers to the length of real-life object Example #1: Finding surface area. Finding surface area of solid figures such as the cube, the cylinder, and so forth is explained here thoroughly.
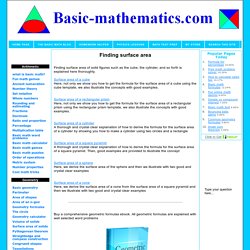
Surface area of a cube Here, not only we show you how to get the formula for the surface area of a cube using the cube template, we also illustrate the concepts with good examples. Surface area of a rectangular prism Here, not only we show you how to get the formula for the surface area of a rectangular prism using the rectangular prism template, we also illustrate the concepts with good examples. Surface area of a cylinder A thorough and crystal clear explanation of how to derive the formula for the surface area of a cylinder by showing you how to make a cylinder using two circles and a rectangle Surface area of a square pyramid A thorough and crystal clear explanation of how to derive the formula for the surface area of a square pyramid.
Then, good examples are provided to illustrate the concept Buy a comprehensive geometric formulas ebook. Volume formulas. Here, we provide you with volume formulas for some common three-dimensional figure Cube: Volume = a3 = a × a × a Cylinder: Volume = pi × r2 × h pi = 3.14 h is the height r is the radius Rectangular solid: Volume = l × w × h.
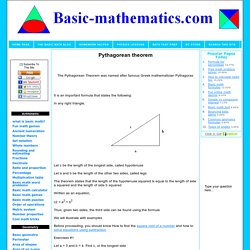
Pythagorean theorem. The Pythagorean Theorem was named after famous Greek mathematician Pythagoras It is an important formula that states the following: In any right triangle,
Ec ss math meas(DETK101138b) Guiding Children's Learning of Mathematics - Leonard Kennedy, Steve Tipps, Art Johnson - Google Books. Transformations and symmetry. Transformations pwrpt. Games. GeometricShapesChart.pdf. Geometry_go_getters.pdf. An introduction to geometry. A point in geometry is a location.
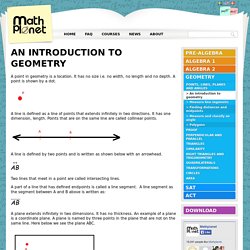
It has no size i.e. no width, no length and no depth. A point is shown by a dot. A line is defined as a line of points that extends infinitely in two directions. It has one dimension, length. Points that are on the same line are called collinear points. A line is defined by two points and is written as shown below with an arrowhead. Two lines that meet in a point are called intersecting lines. Points, Lines, and Planes. Point, line, and plane, together with set, are the undefined terms that provide the starting place for geometry.
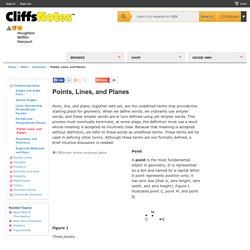
When we define words, we ordinarily use simpler words, and these simpler words are in turn defined using yet simpler words. This process must eventually terminate; at some stage, the definition must use a word whose meaning is accepted as intuitively clear. Because that meaning is accepted without definition, we refer to these words as undefined terms. These terms will be used in defining other terms. Although these terms are not formally defined, a brief intuitive discussion is needed.
Geometry. Geometry is all about shapes and their properties.
If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Point, Line, Plane and Solid A Point has no dimensions, only position A Line is one-dimensional A Plane is two dimensional (2D) A Solid is three-dimensional (3D) Why? Why do we do Geometry? Plane Geometry Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). Perimeter General Drawing Tool Polygons.