

NDE/EMI - Partie 2 : Une percée scientifique majeure - Aux armes citoyens ! L'article précédent [8] proposait une synthèse des données issues des expériences de NDE/EMI.

Après 40 ans de recherches, l'hypothèse d'une conscience externalisée qui mémorise des informations s'est avérée la plus robuste pour expliquer les données collectées. Ce point étant acquis, il justifie la poursuite des recherches à partir de la moisson d'informations contenue dans les témoignages. On va s'intéresser ici à l'aspect "espace temps" de ces expériences en proposant une interprétation dimensionnelle de l'univers perçu lors des NDE, cette approche est basée sur les travaux de Jean Pierre Jourdan [1][2] et Rudy Rucker [3]. Comme on va le voir, ces premières découvertes sont en train de dévoiler un pan entièrement nouveau de la réalité. Une NDE typique présente un scénario récurrent qui peut être totalement ou partiellement mémorisé. (*) Le terme transcendant est impropre car il signifie que l'explication correspondante n'est pas accessible à la science.
Abbot flatland. Dérivées des fonctions. Mathématiques Cours-TD – Culture Scientifique de base – 2005-2006 Chapitre 5 – Fonctions de plusieurs variables.

Pour ce chapitre, on renoncera à écrire des démonstrations : les bases théoriques, les définitions, sont hors de portée de ce programme. On se contentera donc de décrire les calculs, les règles, en mettant en évidence les similitudes avec les fonctions d’une variable. 1) Généralités On connaît la notation (x,y) pour un couple de nombres (ou de n’importe quel élément d’un ensemble), paire ordonnée de ces deux éléments. Comme les fonctions d’une variable réelle sont des correspondances de R dans R, on peut définir les correspondances de R2 dans R, de R3 dans R. Exemples : f(x,y,z)=x+y+z la fonction somme de trois variables ; f(x,y)=xy la fonction produit. La dimension 4, hypercube et compagnie. C’est à partir de la discussion sur SCMB que j’avais envie de faire un petit article ici, à propos des objets en dimension 4.
C’est quoi une dimension au sens mathématique ? La dimension d’un espace c’est le nombre de coordonnées qu’il faut pour repérer un point dans cet espace. Ainsi, en dimension 1 (une demi droite donc) il suffit d’une seule coordonnée pour repérer un point de cette demi-droite par rapport à l’origine. Dans un plan, un point est repéré par deux coordonnées : X et Y : Dans un espace en 3D, comme le monde dans lequel on vit, il faut 3 coordonnées pour se repérer : X, Y et Z généralement. Etude d'une quadrique. Catégorisation. Fonction de plusieurs variables. Un article de Wikipédia, l'encyclopédie libre. .
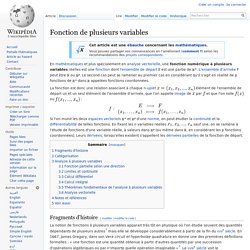
L'ensemble d'arrivée F peut être ou . Champ scalaire. Un article de Wikipédia, l'encyclopédie libre.
Coordonnées cartésiennes. Un article de Wikipédia, l'encyclopédie libre.
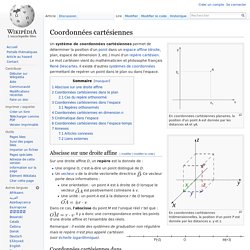
En coordonnées cartésiennes planaires, la position d'un point A est donnée par les distances xA et yA. En coordonnées cartésiennes tridimensionnelles, la position d'un point P est donnée par les distances x, y et z. Abscisse sur une droite affine[modifier | modifier le code] Sur une droite affine D, un repère est la donnée de : Une origine O, c'est-à-dire un point distingué de D.Un vecteur v de la droite vectorielle directrice .
Dans ce cas, l'abscisse du point M est l'unique réel r tel que : . Remarque : Il existe des systèmes de graduation non régulière mais le repère n'est plus appelé cartésien (voir échelle logarithmique). Coordonnées cartésiennes dans le plan[modifier | modifier le code] Dans un plan affine, les coordonnées cartésiennes sont sans doute la manière la plus naturelle de définir un système de coordonnées. Un point d'origine O.deux vecteurs i et j non colinéaires du plan vectoriel directeur . et . Si , il existe un unique n-uplet. Espace de Minkowski. Un article de Wikipédia, l'encyclopédie libre.
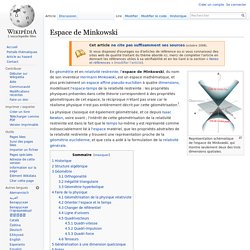
Représentation schématique de l'espace de Minkowski, qui montre seulement deux des trois dimensions spatiales. En géométrie et en relativité restreinte, l’espace de Minkowski, du nom de son inventeur Hermann Minkowski, est un espace mathématique, et plus précisément un espace affine pseudo-euclidien à quatre dimensions, modélisant l'espace-temps de la relativité restreinte : les propriétés physiques présentes dans cette théorie correspondent à des propriétés géométriques de cet espace, la réciproque n'étant pas vraie car le réalisme physique n'est pas entièrement décrit par cette géométrisation[1].
Historique[modifier | modifier le code] Structure algébrique[modifier | modifier le code]