

Reaction-Diffusion Tutorial. The grid is repeatedly updated using the following equations to update the concentrations of A and B in each cell, and model the behaviors described above.
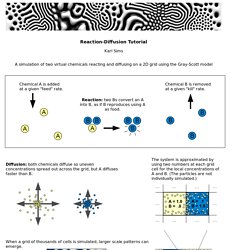
Some typical values used, for those interested, are: DA=1.0, DB=.5, f=.055, k=.062 (f and k vary for different behaviors), and Δt=1.0. The Laplacian is performed with a 3x3 convolution with center weight -1, adjacent neighbors .2, and diagonals .05. The grid is initialized with A=1, B=0, and a small area is seeded with B=1. Surprisingly complex and dynamic behaviors can arise from these fairly simple rules, and adjusting the two parameters for the feed rate and kill rate can produce a range of different results. The grid is visualized by assigning each cell a color from it's A and B values. The reaction naturally has two stable states: lots of A with no B to consume it, or lots of B where new A is quickly converted into more B.
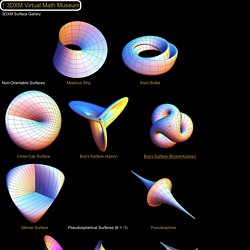
For further information Visit the Reaction-Diffusion Media Wall at the Museum of Science, Boston. Reaction-Diffusion Tutorial. An Introduction to Clustering & different methods of clustering. Implicit Algebraic Surfaces. Gallery of Famous Surfaces. 3DXM Surface Gallery Non-Orientable Surfaces Moebius Strip Klein Bottle Cross-Cap Surface.
MeshMash! « Space Symmetry Structure. As regular readers of this blog will know, I’m passionate about the use of relaxation and force-based methods for optimizing geometry in a very interactive way.
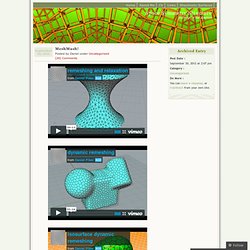
There is a great variety of form-finding that can be done by assigning physical forces as interactions between sets of particles. However, in my investigations so far, the topology of these interactions has usually remained fixed. So the overall shape changes dramatically, but the number of points -and the underlying network of which point interacts with which- remains the same throughout the simulation.
I have written about topology optimization before, in my post on self organizing structures, but the videos above use a fundamentally different approach than any of the examples shown there, as this new work is based on purely local interactions, which reconfigure their connectivity as the geometry changes. edge flip edge collapse edge split. Computational Geometry. User and Reference Manual: Package Overview. Algebraic Foundations Michael Hemmer This package defines what algebra means for CGAL, in terms of concepts, classes and functions.
The main features are: (i) explicit concepts for interoperability of types (ii) separation between algebraic types (not necessarily embeddable into the reals), and number types (embeddable into the reals). Number Types Michael Hemmer, Susan Hert, Sylvain Pion, and Stefan Schirra This package provides number type concepts as well as number type classes and wrapper classes for third party number type libraries.
Modular Arithmetic Michael Hemmer and Sylvain Pion This package provides arithmetic over finite fields. Polynomial This package introduces a concept for univariate and multivariate polynomials in d variables. Algebraic Kernel. Conway polyhedron notation. This example chart shows how 11 new forms can be derived from the cube using 3 operations.
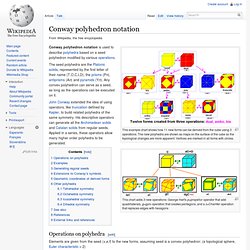
The new polyhedra are shown as maps on the surface of the cube so the topological changes are more apparent. Vertices are marked in all forms with circles. This chart adds 3 new operations: George Hart's p=propellor operator that add quadrilaterals, g=gyro operation that creates pentagons, and a c=Chamfer operation that replaces edges with hexagons Operations on polyhedra[edit] Elements are given from the seed (v,e,f) to the new forms, assuming seed is a convex polyhedron: (a topological sphere, Euler characteristic = 2) Special forms. Hermann Cuntz - homepage. Quadtree. A region quadtree with point data.
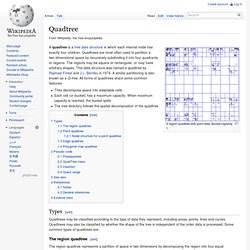
Bucket capacity 1. A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The regions may be square or rectangular, or may have arbitrary shapes. This data structure was named a quadtree by Raphael Finkel and J.L. They decompose space into adaptable cellsEach cell (or bucket) has a maximum capacity.
Types[edit] Quadtrees may be classified according to the type of data they represent, including areas, points, lines and curves. The region quadtree[edit] About. Rhombic Structures. Surface Logic « The Mathematica Journal. Building on the preexisting deployment of equation-based surface geometries in architecture, surface logic explores the dialogue between twentieth-century pioneers of reinforced concrete and the contemporary possibilities made accessible by the instrumentation of computation.

Computational modeling of equation-based surfaces opens designers to unprecedented access and design sensibilities driven by parametric variation, differential topological relationship, fabrication techniques, material analysis, and physical performance. Surface Logic Architecture has long been dominated by orthogonal Cartesian principles of design preferring two-dimensional planning and composition. Rheotomic Surfaces « Space Symmetry Structure. These are Rheotomic Surfaces – from the Greek Rheo – flow and Tomos – cut or section (as in tomography) The horizontal sections of these surfaces correspond to the moving equipotential lines of a 2D Laplacian flow, with height mapped to time.
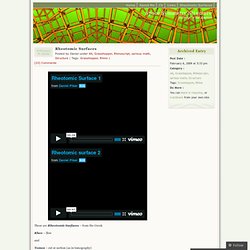
Such surfaces are complete, embedded and walkably connected. In this essay I present a type of mathematically generated surfaces with some unique geometric properties making them particularly well suited for architectural use. I also present some interesting by-products from the development of these surfaces including a novel and simple way of making conformal grids from flows without the usual methods of vector field integration. Finally, I suggest some possible directions for the future development of these ideas, both in architectural and purely geometric fields. Triply Periodic Minimal Surfaces.