

Topology of a Twisted Torus - Numberphile. Visually stunning math concepts which are easy to explain. Art, Mathematics, Music and the Physical Universe. Art, Mathematics, Music and the Physical Universe B.

L. Moiseiwitsch Contents 1. 2. 3. 3.1 Introduction 3.2 Primitive Art 3.3 Music 3.4 Islamic Art 3.5 Renaissance Art 3.6 Modern Art 3.7 Summary 4. 4.1 Geometry 4.2 Time 5. 5.2 Unification of the Forces of Nature 5.5 Space-time and the Uncertainty Principle Appendices Appendix A. Appendix B. Appendix C. Appendix D. Appendix E. References Moonlight Sonata 1. Our knowledge of the external physical universe obviously comes entirely from our senses, mostly by seeing, hearing and touching. As a beginning let us consider the sense of vision. A truly interesting manifestation of this has been produced by the Magic Eye pictures1, or Single Image Random Dot Stereograms, that give rise to remarkable visions of three-dimensional objects by employing coloured dots, the ‘Salitsky Dots’, on a flat piece of paper.
As in the case of vision, there are no actual sounds in the physical world. Ellipticité (géométrie) Foundations and Structure of Mathematics 1 "The Platonic Solids" webpage. Introduction and History The text states that "symmetry and regularity lie at the heart of classical beauty.
" They claim that the most symmetrical object in the plane is a circle. If we require objects to have straight sides and seek symmetry, then we are lead to regular polygons. For any natural number n greater than or equal to 3 ("counting number"), there is a regular polygon with n sides: Notice that as n gets larger, the regular polygon looks more and more like a circle. Geometry: Requirements for a Visualization System for 2020. In this essay, i give a list of requirements that i think is necessary for a software system for creating scientific visualization for the next decade.
For the past 10 years, i have been strongly interested in mathematical visualization. I'm not a professor, and am not doing it for the educational purposes per se. Geometry has just been beautiful for me, and i'm also a professional programer. Programing computers to visualize geometric theorems or geometric objects, has been a immense personal pleasure. Model. Ch. 4 Model We live on the earth, and we know it is a sphere.
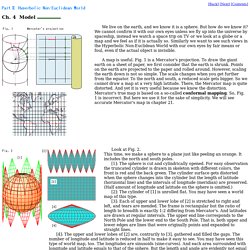
But how do we know it? We cannot confirm it with our own eyes unless we fly up into the universe by spaceship, instead we watch a space trip on TV or we look at a globe or a map and we feel as if it is actually so. Similarly we want to see such views in the Hyperbolic Non-Euclidean World with our own eyes by fair means or foul, even if the actual object is invisible. Math in the Media. "Cuddly Topology" was the caption chosen by Nature's Emma Maris for this image, part of its 2008 Gallery of "the year's most eye-catching science" (December 17, 2008).

Hiding behind curvature. Spherical Projections. Steven Dutch, Natural and Applied Sciences, University of Wisconsin - Green Bay First-time Visitors: Please visit Site Map and Disclaimer.

Use "Back" to return here. Note: Some texts regard the projection plane for some spherical projections as passing through the center of the sphere rather than tangent to it as this page does. Miscellaneous news and sphere eversion. Before we begin, there are a few late items of news worth discussing: There is a free edition of Wolfram Mathematica for the Raspberry Pi, an increasingly popular versatile low-cost computer.
More details are available over at The Aperiodical.The first round of the British Mathematical Olympiad has taken place. Marking is scheduled for the forthcoming weekend, and high scores will be published soon after. Until then, you can see the questions on Joseph Myers’ website.The TMS Call My Bluff (mentioned during the previous cp4space post) was won by the freshers’ team.
Perfect imaging. Perfect imaging is the ability to see minute details with unlimited sharpness.
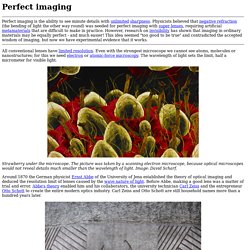
Physicists believed that negative refraction (the bending of light the other way round) was needed for perfect imaging with super lenses, requiring artificial metamaterials that are difficult to make in practice. Projection of Circle onto Spherical Surface. FITS WCS Projections: CSC: COBE quadrilateralized Spherical Cube. This equal area projection shows an entire sphere with a minimum of distortion by projecting it onto the six faces of a cube.

The faces are stored as the third dimension of the image and numbered, contrary to the 1-based FITS convention, 0-5 as shown in the diagram above. This projection was developed to archive data from the COBE (COsmic Background Explorer) satellite. SIMPLE = T / file does conform to FITS standard BITPIX = -32 / number of bits per data pixel NAXIS = 3 / number of data axes NAXIS1 = 128 / length of data axis 1 NAXIS2 = 128 / length of data axis 2 NAXIS3 = 6 / length of data axis 3 CTYPE1 = 'RA---CSC' CTYPE2 = 'DEC--CSC' CTYPE3 = 'CUBEFACE' CRPIX1 = 64.5 / reference pixel CRPIX2 = 64.5 / reference pixel CRVAL1 = 0.0 / reference pixel value CRVAL2 = 0.0 / reference pixel value CDELT1 = -0.703125 / degrees/pixel CDELT2 = 0.703125 / degrees/pixel.
An Interactive Exploration of 3D Surfaces for Public Audiences. Stereographic Projection - Math Images. From Math Images Stereographic Projection of a Sphere Stereographic projection maps each point on a sphere onto a plane.
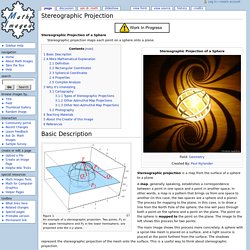
Figure 1An example of a stereographic projection. Two points, P1 in the upper hemisphere and P2 in the lower hemisphere, are projected onto the x-y plane. Stereographic projection is a map from the surface of a sphere to a plane. Projections and Coordinate Systems. Projections and Coordinate Systems Discussion Projections and coordinate systems are a complicated topic in GIS, but they form the basis for how a GIS can store, analyze, and display spatial data. Understanding projections and coordinate systems important knowledge to have, especially if you deal with many different sets of data that come from different sources. ProjectionsDistortionCoordinate SystemsDatumsExamples of different projections Projection Storage vs.
DefinitionProjecting spatial datasetsHow projections work on a programmatic level. Calculer le coté d'un pentagone régulier, exercice de géométrie - 207204. Archimedes on Spheres and Cylinders. So one of the most famous cities in the Greek world, and in former days a great center of learning as well, would have remained in total ignorance of the tomb of the most brilliant citizen it had ever produced, had a man from Arpinum not come and pointed it out! But now to return to the point where I started that digression. Surely anyone who has even the slightest connexion with the Muses, that is to say with civilization and learning, would rather be the mathematician Archimedes than the tyrant Dionysius. Dodecahedron and Icosahedron. The regular dodecahedron and icosahedron The regular dodecahedron In Golden section - Pentagon - Dodecahedron I have explained how a regular dodecahedron can be constructed starting from a cube and what relation exists between the edge of this dodecahedron and the edge of the given cube.
Cylinders in Spheres. What is the largest cylinder that is possible to fit inside a sphere? Let me make that a little clearer. SAT Subject Test: Math Level 2: Inscribed Solids. Inscribed Solids An inscribed solid is a solid fit inside another solid, with the edges of the two solids touching. The figures below are, from left to right, a cylinder inscribed in a sphere, a sphere inscribed in a cube, and a rectangular solid inscribed in a sphere. Math IIC questions that involve inscribed solids don’t require any additional techniques than those you’ve already learned.
What these questions do require is an ability to visualize inscribed solids and the awareness of how certain line segments relate to both solids in a given figure. How to find the side of the largest cube completely contained inside a regular tetrahedron of side s - Quora. Circumscribed sphere. 013 Insciribed and circumscribed sphere about a cube - volume comparison. Polyèdre tronqué. POLYÈDRE TRONQUÉ (AUX SOMMETS)edge-truncated polyhedron, abgestumpftes Polyeder Exemples : les 5 polyèdres réguliers fournissent, par troncature forte ou faible, 7 des 13 polyèdres archimédiens : Les polyèdres obtenus par troncature des polyèdres semi-réguliers ne sont plus semi-réguliers, mais certains sont équivalents à des polyèdres semi-réguliers :
TechnologyUK - Mathematics - Geometry - The Solid Angle. Imagine a huge sphere, painted white on the inside. Next imagine a glass cube, somewhat smaller than the sphere, but floating within it in a central position. Finally imagine yourself floating at the exact centre of the sphere, looking out through the walls of the glass cube. Usin AM-GH inequality to find theMaximum Cylinder Inscribed in a Sphere. From Wolfram MathWorld. From Wolfram MathWorld. Famous space curves in geometry history? Heart Curve. What is the Heart Curve? Spirographs and the third dimension. The basic geometric ideas are straight lines and circles. The famous compass and straight edge. Surfaces mathématiques. One man's Funnies: Mathematical equations of love, heart, penis and the boomerang.
From Wolfram MathWorld. Supershapes / SuperFormula. Geometry, Surfaces, Curves, Polyhedra. Polyhedra deriving from the progressive truncation by cube of the Archimedean truncated tetrahedron and relative duals. Adhering to God's Plan in a Global Society. Dual polyhedron. COGNITIVE GEOMETRICS - GEOMETRY: Dual Polyhedron. Mesure d'un angle en 3D. Solve My Maths. Geometry. Map Projections: Polyhedral Maps - part 1. Spherical trigonometry. DGGS - Hans Havlicek: Visualisation - Dupin Cyclides. Serie V. Famous Curves Index. Cyclide de Dupin. Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere - Edward S. Popko.
S_e9rie_2-2_Polygones_r_e9guliers_-_Copie. Astroïde. Surfaces alg briques. Ellipse. Unitary Flow: June 2009. From Wolfram MathWorld. 10 Icosahedra. 4 LES AMOURS DE L EQUERRE ET DU COMPAS. Icosahedral Polyhedra. Polygons, Meshes. Geometry, Surfaces, Curves, Polyhedra. School of Mathematics and Statistics. Dual polyhedron. Building convex polytopes. Euler angles. 3 Dimentional Vector Geometry. Rotation de coordonnées cartésiennes 3D (Euler) (VI) - Aide LabVIEW 2011 - National Instruments. Spherical Geometry - EscherMath. Pack Turtle. Geometry - Regular polygons constructed inside regular polygons. Regular Polygons Project. Hypotrochoïde. Polygones réguliers.
3D extrusion meshing algorithm. Generative Art, 3D Fractals, Creative Computing. Distance Estimated 3D Fractals (III): Folding Space. Klein bottle. Polygon Triangulation - Graphics Programming and Theory. SLIDE Language Specification. Torus. When Worlds Collide: Simulating Circle-Circle Collisions - Tuts+ Game Development Tutorial. Sequin. 3D Graphics with OpenGL - The Basic Theory.