

Nerd 360 Graus. List of regular polytopes. This page lists the regular polytopes in Euclidean, spherical and hyperbolic spaces.
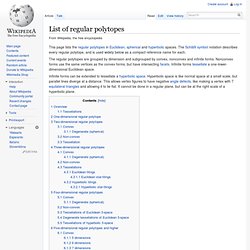
The Schläfli symbol notation describes every regular polytope, and is used widely below as a compact reference name for each. Overview[edit] This table shows a summary of regular polytope counts by dimension. There are no nonconvex Euclidean regular tessellations in any number of dimensions. Platonic solid. History[edit] The Platonic solids have been known since antiquity.
Carved stone balls created by the late neolithic people of Scotland lie near ornamented models resembling them, but the Platonic solids do not appear to have been preferred over less-symmetrical objects, and some of the Platonic solids are even absent.[2] Dice go back to the dawn of civilization with shapes that predated formal charting of Platonic solids. Euclid completely mathematically described the Platonic solids in the Elements, the last book (Book XIII) of which is devoted to their properties. Propositions 13–17 in Book XIII describe the construction of the tetrahedron, octahedron, cube, icosahedron, and dodecahedron in that order. Incidence geometry. Definition[edit]
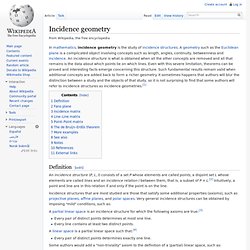
Www.cds.caltech.edu/~marsden/bib/1966/02-BeMaSh1966/BeMaSh1966.pdf. Point at infinity. The real line with the point at infinity. .
The real projective line is not equivalent to the extended real number line, which has two different points at infinity. The point at infinity can also be added to the complex plane, , thereby turning it into a closed surface (i.e., complex algebraic curve) known as the complex projective line, , also called the Riemann sphere. The concept of infinity point admits several generalizations for various multi-dimensional constructions.
Homogeneous space. Formal definition[edit] Succinctly, if X is an object of the category C, then the structure of a G-space is a homomorphism: into the group of automorphisms of the object X in the category C.
Hyperplane. Technical description[edit] Dihedral angles[edit] Special types of hyperplanes[edit] Several specific types of hyperplanes are defined with properties that are well suited for particular purposes.
Some of these specializations are described here. Affine hyperplanes[edit] Www.cis.upenn.edu/~cis610/geombchap2. Affine space. The solution set of an inhomogeneous linear equation is either empty or an affine subspace.
In particular, a point is a zero-dimensional affine subspace. Informal descriptions[edit] p + (a − p) + (b − p). Similarly, Alice and Bob may evaluate any linear combination of a and b, or of any finite set of vectors, and will generally get different answers. However, if the sum of the coefficients in a linear combination is 1, then Alice and Bob will arrive at the same answer. Finite Geometry. 1.2 A Finite Geometry PrintoutAs a basis for our study we assume an arbitrary collection of entities of an arbitrary nature, entities which for brevity, we shall call points, and this quite independently of their nature.— Gino Fano (1871–1952)

Finite geometry. Finite affine plane of order 2, containing 4 points and 6 lines.

Lines of the same color are "parallel". Finite geometries may be constructed via linear algebra, starting from vector spaces over a finite field; the affine and projective planes so constructed are called Galois geometries. Finite geometries can also be defined purely axiomatically. Most common finite geometries are Galois geometries, since any finite projective space of dimension three or greater is isomorphic to a projective space over a finite field (that is, the projectivization of a vector space over a finite field). However, dimension two has affine and projective planes that are not isomorphic to Galois geometries, namely the non-Desarguesian planes. Incidence geometry. Incidence (geometry) Historically, projective geometry was introduced in order to make the propositions of incidence true (without exceptions such as are caused by parallels).
From the point of view of synthetic geometry it was considered that projective geometry should be developed using such propositions as axioms. This turns out to make a major difference only for the projective plane (for reasons to do with Desargues' theorem). The modern approach is to define projective space starting from linear algebra and homogeneous co-ordinates. Then the propositions of incidence are derived from the following basic result on vector spaces: given subspaces U and V of a vector space W, the dimension of their intersection is at least dim U + dim V − dim W. Let L1 and L2 be a pair of lines, both in a projective plane and expressed in homogeneous coordinates: which maps lines onto their dual points.
Let P1 and P2 be a pair of points, both in a projective plane and expressed in homogeneous coordinates: is true. Proof. Curvature of a sphere. Spherical Triangle. A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices. The spherical triangle is the spherical analog of the planar triangle, and is sometimes called an Euler triangle (Harris and Stocker 1998). Tessellation. Ceramic Tiles in Marrakech, forming edge-to-edge, regular and other tessellations A periodic tiling has a repeating pattern. Some special kinds include regular tilings with regular polygonal tiles all of the same shape, and semi-regular tilings with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. Coxeter–Dynkin diagram. Coxeter–Dynkin diagrams for the fundamental finite Coxeter groups Coxeter–Dynkin diagrams for the fundamental affine Coxeter groups Each diagram represents a Coxeter group, and Coxeter groups are classified by their associated diagrams.
Dynkin diagrams are closely related objects, which differ from Coxeter diagrams in two respects: firstly, branches labeled "4" or greater are directed, while Coxeter diagrams are undirected; secondly, Dynkin diagrams must satisfy an additional (crystallographic) restriction, namely that the only allowed branch labels are 2, 3, 4, and 6. See Dynkin diagrams for details. Dynkin diagrams correspond to and are used to classify root systems and therefore semisimple Lie algebras.[1] List of convex uniform tilings.
This table shows the 11 convex uniform tilings (regular and semiregular) of the Euclidean plane , and their dual tilings. There are three regular, and eight semiregular, tilings in the plane. The semiregular tilings form new tilings from their duals, each made from one type of irregular face. Uniform tilings are listed by their vertex configuration , the sequence of faces that exist on each vertex. For example means one square and two octagons on a vertex. File:Pythagorean proof (1).svg. The original description page is/was here. All following user names refer to en.wikipedia. 2010-07-15 04:40 Phildonnia 744×1052× (28485 bytes) {{Information |Description = |Source = I (~~~) created this work entirely by myself.
|Date = ~~~~~ |Author = ~~~ |other_versions = }} Click on a date/time to view the file as it appeared at that time. Differential geometry of surfaces. In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. Algebraic geometry. Differential geometry of surfaces. Riemannian geometry. Riemannian manifold. Manifold. The surface of the Earth requires (at least) two charts to include every point. Here the globe is decomposed into charts around the North and South Poles.