

3-D Fractals Offer Clues to Complex Systems. If you came across an animal in the wild and wanted to learn more about it, there are a few things you might do: You might watch what it eats, poke it to see how it reacts, and even dissect it if you got the chance.
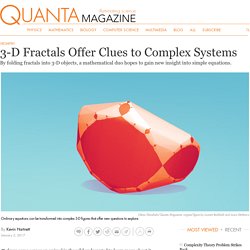
Mathematicians are not so different from naturalists. Rather than studying organisms, they study equations and shapes using their own techniques. They twist and stretch mathematical objects, translate them into new mathematical languages, and apply them to new problems. The golden ratio has spawned a beautiful new curve: the Harriss spiral. Mathematicians like to come up with new stuff.
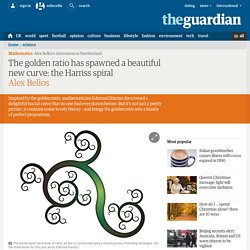
A theorem, perhaps, a lemma or even just a corollary. Edmund Harriss discovered a curve. Harriss teaches maths at the University of Arkansas. He’s also an artist and his intellectual quest began with a shape that famously belongs to both science and art: the golden rectangle: A golden rectangle is a rectangle whose sides are proportioned according to the golden ratio, which is 1.618. What is particularly interesting, however, about a golden rectangle is that if you draw a square inside it, as above, the remaining section (in blue) is a smaller golden rectangle. Logic - the fractal or scale-free middle of a hierarchy. What is a fractal?

And why does it matter? A fractal shape is geometry with scale – a middle ground or internal axis of scale symmetry. So it is no surprise that fractals should turn out to model an organic world which is based on a logic of growth and hierarchical scale. Ordinary geometry – like ordinary logic or ordinary science – does not take account of scale. Differences in size are not seen as something fundamental. Fractal and Transfractal Scale-Free Networks. Benoit Mandelbrot - Hunting the Hidden Dimension Nova (2008) Arthur C Clarke - Fractals - The Colors Of Infinity. 100 - Fractal Geometry. Geometry.
Its principles are taught to young students across the world. The Pythagorean theorem. Surface area and volume. Pi. This classical, or Euclidean, geometry is perfectly suited for the world that humans have created. In 1961, Benoit Mandelbrot was working as a research scientist at the Thomas J. Benoit Mandelbrot: Fractals and the art of roughness. Mandelbrot Maps. Fractal Science Kit - Fractal Generator. Fractals (VLab: Virtual Complexity Lab) Author: Greg Paperin.

Fractals are, roughly speaking, objects that exhibit self-similarity on all scales. Self-similarity means that an object consists of smaller copies if itself, which in turn, consist of smaller copies, and so on. The copies do not need to be exact, but the same kind of structures must appear on all scales. Commonly, fractals are mathematical objects, but many natural objects that demonstrate self-similarity on power-law scales are also considered fractals. This includes surfaces of clouds, mountains and other landscape entities, surfaces of plant structures and various other phenomena. Fractal dimensions Intuitively, a fractal is a very rough or winded object – so rough that its surface “breaks out” of its dimension. The above process seems intuitive for all objects. The resulting set of points exhibits some fascinating properties typical of fractals: For instance, we have removed 25% of the remaining area of the structure at each step.
Mandelbulb: The Unravelling of the Real 3D Mandelbrot Fractal. Opening Pandora's Box For the Second Time ur story starts with a guy named Rudy Rucker, an American mathematician, computer scientist and science fiction author (and in fact one of the founders of the cyberpunk science-fiction movement).

Around 20 years ago, along with other approaches, he first imagined the concept behind the potential 3D Mandelbulb (barring a small mistake in the formula, which nevertheless still can produce very interesting results - see later), and also wrote a short story about the 3D Mandelbrot in 1987 entitled "As Above, So Below" (also see his blog entry and notebook).
Back then of course, the hardware was barely up to the task of rendering the 2D Mandelbrot, let alone the 3D version - which would require billions of calculations to see the results, making research in the area a painstaking process to say the least. So the idea slumbered for 20 years until around 2007. Zooming in reveals some interesting detail, but nothing truly fantastic. Full size shown here. 3D Fractal Box Menger Box 1 - HD 720p - Mandelbulb 3D anaglyph stereo. Mathematical Art Galleries. Orbital Fern. The Bizarre Object We Believed Was Impossible to Visualize. Well I wouldn't suggest you chop your fingers off like Django.
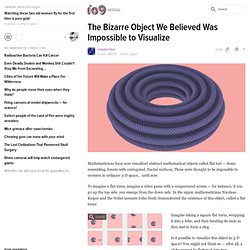
But the rest of it yes I suggest you try to write. Also I as a Humanities major don't really understand this but it does sound cool. I'm an engineering major, and I still don't get it. Maybe if it was written in my first language... Well I assume at some point the article will be translated or some popular science magazine will explain it all in your native tongue. But basically, if I understand it correctly, what's being described here is something like the toridal equivalent of a pseudosphere. Well, in reply to the losing fingers in a fire example, I could say that I'm not expecting people to take up complex variable analysis of poles and residues as a hobby but— They can at least try to read some articles of these interesting discoveries in math written for general audiences. An Introduction to the fascinating patterns of Visual Math. Fractalforums.com - Welcome to Fractal Forums - Index.
Fractal Geometry.