

Math 101: A reading list for lifelong learners. Ready to level up your working knowledge of math?

Here’s what to read now — and next. Math 101, with Jennifer Ouellette First, start with these 5 books… SAT Subject Test: Math Level 2: Triangles. Triangles You will need a solid understanding of triangles in order to answer other questions about polygons, coordinate geometry, and trigonometry.
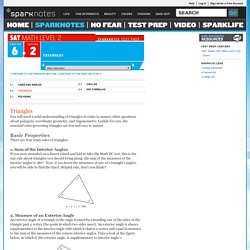
Luckily for you, the essential rules governing triangles are few and easy to master. Basic Properties There are four main rules of triangles: 1. Faculty.uncfsu.edu/dwallace/lesson 16.pdf.
Hammack Home. This book is an introduction to the standard methods of proving mathematical theorems.

It has been approved by the American Institute of Mathematics' Open Textbook Initiative. Also see the Mathematical Association of America Math DL review (of the 1st edition), and the Amazon reviews. How Mathematics Can Make Smart People Dumb - Ben O'Neill. Mathematics can sometimes make smart people dumb.
Let me explain what I mean by this. I don't mean that it is dumb not to be good at mathematics. After all, mathematics is a highly abstract and challenging discipline requiring many years (decades even) of study, and there are plenty of very smart people who have little understanding of it, and little ability to use it. What I mean is that mathematics quite often bamboozles people into accepting very silly arguments — arguments that are so silly that if you stated them without draping them in mathematical negligee, you would instantly become an object of ridicule to all those people who flunked out at basic algebra back in high school. Home. Euler's identity. The exponential functionez can be defined as the limit of (1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of (1 +iπ/N)N.
In this animation N takes various increasing values from 1 to 100. Augustin-Louis Cauchy. Baron Augustin-Louis Cauchy (French: [oɡystɛ̃ lwi koʃi]; 21 August 1789 – 23 May 1857) was a French mathematician who was an early pioneer of analysis.
Binomial theorem. In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. When an exponent is zero, the corresponding power is usually omitted from the term. For example, Ramsey theory. This article is a non-technical introduction to the subject.
For the main encyclopedia article, see Ramsey's theorem. Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear. Set theory. The modern study of set theory was initiated by Georg Cantor and Richard Dedekind in the 1870s.
After the discovery of paradoxes in naive set theory, numerous axiom systems were proposed in the early twentieth century, of which the Zermelo–Fraenkel axioms, with the axiom of choice, are the best-known. Set theory is commonly employed as a foundational system for mathematics, particularly in the form of Zermelo–Fraenkel set theory with the axiom of choice. Beyond its foundational role, set theory is a branch of mathematics in its own right, with an active research community. Contemporary research into set theory includes a diverse collection of topics, ranging from the structure of the real number line to the study of the consistency of large cardinals. History[edit] Mathematical topics typically emerge and evolve through interactions among many researchers. Cantor's work initially polarized the mathematicians of his day. Basic concepts and notation[edit] Some ontology[edit] Sets alone.
Grelling–Nelson paradox. The Grelling–Nelson paradox is a semantic self-referential paradox formulated in 1908 by Kurt Grelling and Leonard Nelson and sometimes mistakenly attributed to the German philosopher and mathematician Hermann Weyl.[1] It is thus occasionally called Weyl's paradox as well as Grelling's paradox.
It is closely analogous to several other well-known paradoxes, in particular the barber paradox and Russell's paradox. The paradox[edit] Suppose one interprets the adjectives "autological" and "heterological" as follows: An adjective is autological (sometimes homological) if and only if it describes itself. For example "short" is autological, since the word "short" is a short word. All adjectives, it would seem, must be either autological or heterological, for each adjective either describes itself, or it doesn't.
Mathematical Association of America. Mathematical Sculptures Made Out Of Office Supplies (PHOTOS) "I think about math constantly and I see and look for math in everything around me. " Zachary Abel is a second year Ph.D student in the MIT Mathematics department, but he also creates sculptures out of everyday objects. "By transforming often-overlooked household items into elaborate, mathematical sculptures, I hope to share this sense of excitement, curiosity, and beauty that a mathematical outlook has instilled in me.
" Zachary Abel, "Impenetraball", 2011. The "Impenetraball" protects its hollow interior with a dense, chainmail-like mesh made from 132 binder clips (and pliers). With his intricate formations of otherwise mundane objects, Abel hopes to expose the "hidden geometric beauty" in our everyday lives. MAA Focus October/November 2010. Vi Hart: Blog. Algebraic Surfaces Gallery. Calculus Video Tutorials.