Quaternary numeral system. It shares with all fixed-radix numeral systems many properties, such as the ability to represent any real number with a canonical representation (almost unique) and the characteristics of the representations of rational numbers and irrational numbers.
See decimal and binary for a discussion of these properties. Relation to other positional number systems[edit] Relation to binary[edit] As with the octal and hexadecimal numeral systems, quaternary has a special relation to the binary numeral system. Each radix 4, 8 and 16 is a power of 2, so the conversion to and from binary is implemented by matching each digit with 2, 3 or 4 binary digits, or bits. Although octal and hexadecimal are widely used in computing and computer programming in the discussion and analysis of binary arithmetic and logic, quaternary does not enjoy the same status.
By analogy with bit, a quaternary digit is sometimes called a crumb. Occurrence in human languages[edit] Hilbert curves[edit] Genetics[edit] Duodecimal. The number twelve, a superior highly composite number, is the smallest number with four non-trivial factors (2, 3, 4, 6), and the smallest to include as factors all four numbers (1 to 4) within the subitizing range.
As a result of this increased factorability of the radix and its divisibility by a wide range of the most elemental numbers (whereas ten has only two non-trivial factors: 2 and 5, with neither 3 nor 4), duodecimal representations fit more easily than decimal ones into many common patterns, as evidenced by the higher regularity observable in the duodecimal multiplication table.
Sexagesimal. Origin[edit] It is possible for people to count on their fingers to 12 using one hand only, with the thumb pointing to each finger bone on the four fingers in turn.
A traditional counting system still in use in many regions of Asia works in this way, and could help to explain the occurrence of numeral systems based on 12 and 60 besides those based on 10, 20 and 5. In this system, the one (usually right) hand counts repeatedly to 12, displaying the number of iterations on the other (usually left), until five dozens, i. e. the 60, are full.[1][2] Quaternions and spatial rotation. Using quaternion rotations[edit] A Euclidean vector such as (2, 3, 4) or (ax, ay, az) can be rewritten as 2 i + 3 j + 4 k or ax i + ay j + az k, where i, j, k are unit vectors representing the three Cartesian axes.
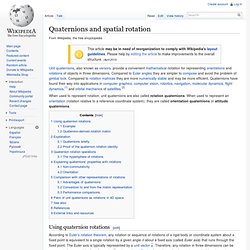
A rotation through an angle of θ around the axis defined by a unit vector is represented by a quaternion using an extension of Euler's formula: The rotation is clockwise if our line of sight points in the same direction as u→. It can be shown that this rotation can be applied to an ordinary vector in 3-dimensional space, considered as a quaternion with a real coordinate equal to zero, by evaluating the conjugation of p by q: using the Hamilton product, where p′ = (px′, py′, pz′) is the new position vector of the point after the rotation. Curious quaternions.
November 2004 John Baez is a mathematical physicist at the University of California, Riverside.
He specialises in quantum gravity and n-categories, but describes himself as "interested in many other things too. " His homepage is one of the most well-known maths/physics sites on the web, with his column, This Week's Finds in Mathematical Physics, particularly popular. In a two-part interview this issue and next, Helen Joyce, editor of Plus, talks to Baez about complex numbers and their younger cousins, the quaternions and octonions. The birth of complex numbers Like many concepts in mathematics, complex numbers first popped up far from their main current area of application.
The birth of the complex The particular challenge that brought mathematicians to consider what they soon called "imaginary numbers" involved attempts to solve equations of the type ax2+bx+c=0. The complex number with real part 1 and imaginary part 2 where and are just plain honest to goodness numbers. Quaternion. Graphical representation of quaternion units product as 90°-rotation in 4D-space, ij = k, ji = −k, ij = −ji History[edit] Quaternion plaque on Brougham (Broom) Bridge, Dublin, which says: Here as he walked by on the 16th of October 1843 Sir William Rowan Hamilton in a flash of genius discovered the fundamental formula for quaternion multiplicationi2 = j2 = k2 = ijk = −1 & cut it on a stone of this bridge Quaternion algebra was introduced by Hamilton in 1843.[7] Important precursors to this work included Euler's four-square identity (1748) and Olinde Rodrigues' parameterization of general rotations by four parameters (1840), but neither of these writers treated the four-parameter rotations as an algebra.[8][9] Carl Friedrich Gauss had also discovered quaternions in 1819, but this work was not published until 1900.[10][11] i2 = j2 = k2 = ijk = −1, into the stone of Brougham Bridge as he paused on it.