

Gaussian Skirmish. I have a particular fondness for Gauss, as he was my entry into math history.John Hocking, whom I usually refer to as my undergraduate math guru, was, by great fortune, my math teacher for the first two years at Michigan State.
A good researcher himself, he brought math alive with deep connections, intriguing applications, lively stories of discovery and some history of the great mathematicians. It had never really occurred to me to wonder who invented the stuff we were studying. Unthinkable in most other subjects.But when Karl Friedrich Gauss came up, the usually passionate Gibb kicked it into another gear. Complex Projective 4-Space. A most delightful way to procrastinate is to attempt the unsolved problems on MathOverflow.
Especially rewarding is when you actually end up solving such a problem, or when you learn something in the process, or both. Last night I learnt the terms golygon (coined by Lee Sallows) and golyhedron (coined by Joseph O’Rourke before their existence had even been established), eventually providing an example of the latter after a reasonable amount of work. Fullerenes, Fibonacci Walks, and a Fourier Toy. Welcome to this week’s Math Munch!
Stan and James Earlier this month, neuroscientists Stan Schein and James Gayed announced the discovery of a new class of polyhedra. How Quadratic Reciprocity Is Like Dealing Cards. Currently the Riemann-Roch theorem is my nemesis, and I stumbled on Matt Baker’s math blog while I was looking for some help understanding figuring out how to use it.

The post I came across, Riemann-Roch for Graphs and Applications, was not what I was looking for, but I’m glad I found it! Baker, a math professor at Georgia Tech, describes the Riemann-Roch theorem for graphs in fairly straightforward language and also gives some background about how he and his coauthor Serguei Norine discovered it. At the beginning it was a theorem in search of a precise formulation: “I stumbled upon the idea that there ought to be a graph-theoretic avatar of the Riemann-Roch Theorem while investigating ‘p-adic Riemann surfaces’ (for the experts: Berkovich curves). Part of Baker’s explanation of quadratic reciprocity using cards. Image: Matt Baker. Another post that caught my eye, probably because of the pictures, was Quadratic Reciprocity and Zolotarev’s Lemma.
Quadratic reciprocity and Zolotarev’s Lemma. I want to explain a beautiful proof of the Law of Quadratic Reciprocity from c. 1874 due to Egor Ivanovich Zolotarev (1847-1878).
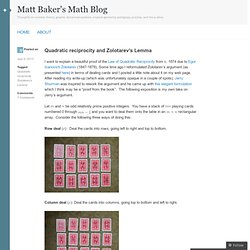
Some time ago I reformulated Zolotarev’s argument (as presented here) in terms of dealing cards and I posted a little note about it on my web page. After reading my write-up (which was unfortunately opaque in a couple of spots), Jerry Shurman was inspired to rework the argument and he came up with this elegant formulation which I think may be a “proof from the book”. The following exposition is my own take on Jerry’s argument. Graph Theory, Part 2. Ok, I’m still really overly excited about Graph Theory (and teaching in a way more aligned to my philosophy!).
While Kogut and I were at the AERA conference, my awesome student teachers led students through the Bridges of Konigsberg and the beginning of a snowplow route project, where students had to find a more efficient route through a neighborhood (in the future … smaller neighborhoods!). Graph Theory, Part 1. The last unit for my senior class (Advanced Math Decision Making) is Networks and Graph Theory.
Win for me (and hopefully the students)! My student teachers and I are taking the opportunity to teach a little more like I want to next year (my student teachers are amazing). Here’s how we’ve done, so far. Day 1: We started by challenging the students to find a Eulerian path and circuit through the basement (we didn’t use that language). And then took them to the basement. They explored in groups of ~3, at first with only the criteria for a path/circuit and then with a map. Day 2: We started this day by naming our circuits and paths. Find It! Design The call: a game for 5th graders just starting with fraction multiplication.
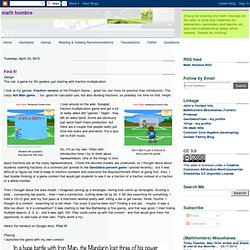
I look at my games. Fraction version of the Product Game... great fun, but more for practice than introduction. The crazy Ant Man game ... fun, good for calculator use, but also dividing fractions, so probably not time for that. Hmph. I look around on the web. So, I'm on my own. Then I thought about the area model. Here's the handout on Google docs: Find It! Playing I launched the game with my own context: They managed to find all three, before... well before nothing.
Turning pants inside-out (or backwards) while tied together. Current community your communities Sign up or log in to customize your list. more stack exchange communities Stack Exchange sign up log in tour help MathOverflow Ask Question Take the 2-minute tour ×
Euler Zigzag Numbers (Alternating Permutations) - Robert Dickau. The numbers of alternating permutations (permutations in which the difference between each successive pair of adjacent elements changes sign—that is, each “rise” is followed by a “fall”, and vice versa) for n elements are sometimes called the Euler zigzag numbers.

For the list {1, 2, 3}, the permutation {1, 3, 2} is an alternating permutation, while {3, 2, 1} is not. Determining the number of alternating permutations of the elements {1, 2, …, n} is called André’s Problem. The following examples illustrate only the alternating permutations that begin with a “rise”; we can get all the permutations that begin with a “fall” by flipping the images vertically. Math Teachers at Play 61. Researching 61 as a number tells us it's not just prime, but is a twin prime, a cuban prime, the 9th Mersenne prime exponent, and a Pillai prime.
That's primo prime pedigree. It's a Keith number and thrice Fortunate. (Fortunate numbers are pretty interesting and the subject of an open conjecture.)