

Boundary (topology) Metric space. The most familiar metric space is 3-dimensional Euclidean space.
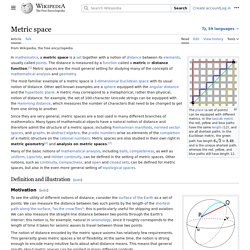
In fact, a "metric" is the generalization of the Euclidean metric arising from the four long-known properties of the Euclidean distance. The Euclidean metric defines the distance between two points as the length of the straight line segment connecting them. Other metric spaces occur for example in elliptic geometry and hyperbolic geometry, where distance on a sphere measured by angle is a metric, and the hyperboloid model of hyperbolic geometry is used by special relativity as a metric space of velocities. History[edit] Maurice Fréchet introduced metric spaces in his work Sur quelques points du calcul fonctionnel, Rendic. Mathematics. Mathematics (from Greek μάθημα máthēma, “knowledge, study, learning”) is the study of topics such as quantity (numbers),[2] structure,[3] space,[2] and change.[4][5][6] There is a range of views among mathematicians and philosophers as to the exact scope and definition of mathematics.[7][8] Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements.
Since the pioneering work of Giuseppe Peano (1858–1932), David Hilbert (1862–1943), and others on axiomatic systems in the late 19th century, it has become customary to view mathematical research as establishing truth by rigorous deduction from appropriately chosen axioms and definitions. Mathematics developed at a relatively slow pace until the Renaissance, when mathematical innovations interacting with new scientific discoveries led to a rapid increase in the rate of mathematical discovery that has continued to the present day.[11] History.
MiePlot. A computer program for scattering of light from a sphere using Mie theory & the Debye series MiePlot was originally designed to provide a simple interface (for PCs using Microsoft Windows) to the classic BHMIE algorithm for Mie scattering from a sphere - as published by Bohren and Huffmann in "Absorption and scattering of light by small particles" (ISBN 0-471-29340-7).
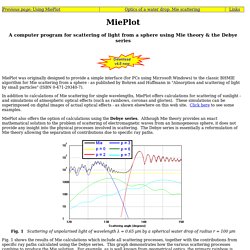
In addition to calculations of Mie scattering for single wavelengths, MiePlot offers calculations for scattering of sunlight - and simulations of atmospheric optical effects (such as rainbows, coronas and glories). These simulations can be superimposed on digital images of actual optical effects - as shown elsewhere on this web site. Click here to see some examples. MiePlot also offers the option of calculations using the Debye series. CFD-Wiki, the free CFD reference. From CFD-Wiki The Navier-Stokes equations are the basic governing equations for a viscous, heat conducting fluid.
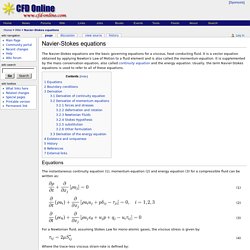
It is a vector equation obtained by applying Newton's Law of Motion to a fluid element and is also called the momentum equation. It is supplemented by the mass conservation equation, also called continuity equation and the energy equation. Usually, the term Navier-Stokes equations is used to refer to all of these equations. Jonathan M. Cohen. Tutorials related to Kinematic Mechanisms. The Math Forum - Ask Dr. Math. Ask Dr.
Math® Thank you for your interest in Ask Dr. Math. We are no longer accepting new questions for this service. The archives of Dr. La structure de Weaire et Phelan. Lorsque les manchots empereurs, un œuf posé sur leurs pattes, bravent le froid en attendant que madame rapporte sa pêche, ils se serrent les uns contre les autres en un grand cercle mouvant ; ceux du bord s’insèrent pour se retrouver progressivement au centre, et ainsi de suite pour ne pas mourir de froid.

Cette position des manchots s’appelle la tortue. Sa forme circulaire est optimale, elle minimise la proportion de manchots sur le bord. Pour un nombre de manchots donné, le cercle minimise donc le nombre d’entre eux qui sont sur le pourtour de la zone occupée et ne peuvent se réchauffer au contact de leurs voisins. En termes mathématiques, si une courbe tracée dans le plan entoure une aire fixée A, son périmètre est toujours supérieur à celui d’un cercle entourant un disque de même aire A. La forme d’une bulle de savon s’adapte librement pour minimiser son énergie. Cependant les bulles ne sont pas toujours rondes. Double Bulle Figure réalisée par John Sullivan. Associaèdre. Un ballon de foot fractal. On a vu le Mandelbulb, le Mandelbox et voici maintenant une toute autre famille d’objets fractals. [1] Cette fois-ci, ce sont des polyèdres : les solides de Platon et des solides d’Archimède, mais aussi quelques formes plus exotiques.
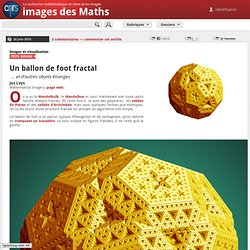
On va les munir d’une structure fractale en utilisant un algorithme très simple. Images des mathématiques. Éponge de Menger. Un article de Wikipédia, l'encyclopédie libre.
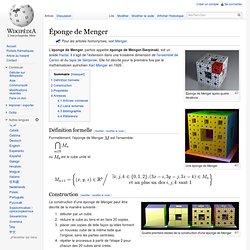
Pour les articles homonymes, voir Menger. Bathsheba Sculpture. Rapid Prototyping Models. Background Rapid Prototyping or Solid Freeform Fabrication refers to a range of new technologies which construct physical three-dimensional objects by assembling thin layers of material under computer control.

Objects can be made which are extremely accurate, complex, and beautiful, and which no other technology can produce. For basic information on this rapidly evolving technology, I recommend this site or this site or search Google for new developments. Presently this is a somewhat expensive technology used mainly in high-end product design, and in research universities.
But in the future, the cost will certainly come down and everyone will be able to create amazing physical objects with these machines. Color Shaded Relief - Grid.