

DevCpp.pdf. Coursurlesarbres1.pdf. AP-algo.pdf. Cours4&5arbresExpressions. 7-trees.pdf. S2recursivite.pdf. Chapcreux2014.pdf. Parcours_arbre_avec_solutions-2.pdf. ALGORITHMIQUE I: Parcours d'un arbre binaire : préfixé, infixé, postfixé. Sommaire Problème et modélisation.

Dans toute la suite A désigne un arbre binaire enraciné. On veut réaliser une opération à chaque donnée rangée dans les différents nœuds de l'arbre. La question qui se pose est : comment accéder à l'ensemble des données de l'arbre ? Description des algorithmes. Les trois parcours préfixé, infixé et postfixé correspondent à des positions différentes de l'opération à réaliser par rapport aux deux appels récursifs.
Piles et files. Arbre binaire. Un article de Wikipédia, l'encyclopédie libre.
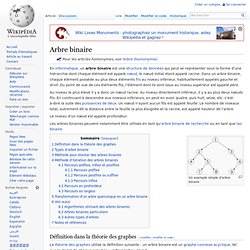
Au niveau le plus élevé il y a donc un nœud racine. Au niveau directement inférieur, il y a au plus deux nœuds fils. En continuant à descendre aux niveaux inférieurs, on peut en avoir quatre, puis huit, seize, etc. c'est-à-dire la suite des puissances de deux. Un nœud n'ayant aucun fils est appelé feuille. Le nombre de niveaux total, autrement dit la distance entre la feuille la plus éloignée et la racine, est appelé hauteur de l'arbre. Le niveau d'un nœud est appelé profondeur. Les arbres binaires peuvent notamment être utilisés en tant qu'arbre binaire de recherche ou en tant que tas binaire. Un exemple simple d'arbre binaire Définition dans la théorie des graphes[modifier | modifier le code]
IR2_2013_parcours.pdf. Chap4.7 : Arbres. 06-Arbres.pdf. Les listes chaînées. Coursalgo.pdf. Bostan10.pdf. 05_LISTESCHAINEES.pdf. Chap5.pdf. 11 Calculer. 11.1 Les nombres premiers Des nombres premiers inférieurs ou égaux à n, il y en a n∕lnn à la limite.

Le crible d’Eratosthène : pour générer tous les nombres premiers inférieur ou égaux à n, partez d’un tableau avec les nombres 2,3,…,n. Puis pour tout i = 2,…,n : si i n’est pas barré, le marquer comme premier, et barrer tous les multiples de i dans le tableau. Une implémentation possible : // au debut tout le monde est premier, sauf 0,1 for (int i=2; i<n; i++) p[i] = true; for (int j=2; j<n; j++) if (p[j]) { // j est premier System.out.print("␣"+j); for (int k=2*j; k<n; k+=j) p[k] = false; // k = multiple de j } Pour tester si un nombre n est premier, il suffit de vérifier qu’il ne peut être divisé par aucun des nombres premiers entre 2 et .
Ceci donne lieu à un algorithme, où on génère une liste L de nombres premiers, et pour chaque i, on teste la primalité en divisant par les entiers de L jusqu’à et on ajoute i à la fin de L, si i est premier. Cours_TDA_Arbin.pdf. Solution : DVDMIAGE_Algo_Chapitre_10_Listes.pdf. Solution. Solution Le nombre n d’éléments à trier est la mesure de la taille des données.

La première observation que l’on peut faire est que chaque ordre d’affectation prend un temps constant, indépendant de la taille des données. Autrement dit, les instructions des lignes (4), (5) et (6) prennent chacune un temps de O(1). Remarquer que O(1) est la transcription en notation O de l’expression ‘’ un temps constant’’. Par la règle de la somme, la complexité conjointe de ce groupe d’instructions est O(max(1,1,1))=O(1). À présent, nous devons prendre en compte les instructions conditionnelles et les boucles. En nous déplaçant vers l’extérieur, nous rencontrons les lignes (2)-(6) de la boucle for. Examinons ensuite la boucle externe, qui contient toutes les instructions exécutables du programme. Matrice creuse. Un article de Wikipédia, l'encyclopédie libre.
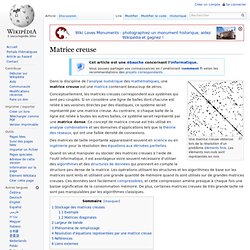
Une matrice creuse obtenue lors de la résolution d'un problème éléments finis. Les éléments non-nuls sont représentés en noir. Conceptuellement, les matrices creuses correspondent aux systèmes qui sont peu couplés. Si on considère une ligne de balles dont chacune est reliée à ses voisines directes par des élastiques, ce système serait représenté par une matrice creuse. Solution pour listes circulaires. Algorithmique : tri et complexité. Algorithmique et Structures de Données I. Objectifs généraux Il s'agit d'une série de travaux dirigés d'algorithmique et structures de données I.Ils ont pour but de : Apprendre à concevoir des algorithmes efficaces indépendamment deslangages ou environnements d’exécution. étudier les types de données etleurs utilisations courantes, à l’aide d’algorithmes adaptés et optimisés.
Acquérir des Bases algorithmiques (affectation, entrées - sorties, structuresconditionnelles, structures itératives et boucles), notion d’emplacementmémoire (Tableaux), procédures, fonctions, passage des paramètres,recherche, tris. Pré-requis. Chap4.6 : Quelques méthodes de tri. Une opération élémentaire est une opération fondamentale d'un algorithme si le temps d'exécution est directement lié (par une formule mathématique ou empirique) au nombre de ces opérations élémentaires.

Il peut y avoir plusieures opérations élémentaires dans un même algorithme. Nb( Iter ) = ( å Nb(ip) + 1 ) . 03-Structures.pdf. Programmation Algorithmique/Listes simplement chaînées. Un livre de Wikilivres. à étoffer, clarrifier, reformuler, etc...
Exemples d'algorithmes. Date de publication : 05/03/2005 , Date de mise a jour : 05/03/2005 Par Selkis (selkis.developpez.com) Dans le cours qui va suivre, nous allons utiliser un pseudo-langage, comportant toutes les structures de base d'un langage de programmation.
04-Tris.pdf. Dichotomie. Un article de Wikipédia, l'encyclopédie libre.
La dichotomie (« couper en deux » en grec) est, en algorithmique, un processus itératif ou récursif de recherche où, à chaque étape, on coupe en deux parties (pas forcément égales) un espace de recherche qui devient restreint à l'une de ces deux parties. L'algorithme s'applique typiquement à la recherche d'un élément dans un ensemble fini ordonné et organisé en séquence. La fonction de « taille » du problème sera alors le cardinal de l'espace (fini) de recherche, et à chaque étape, on coupera l'espace de recherche en deux parties de même taille (à un élément près) de part et d'autre de l'élément médian. Exemple[modifier | modifier le code] Prenons un exemple simple et ludique pour illustrer le mécanisme de recherche par dichotomie : Pour l'exemple de Julie et Paul, il y a N = 101 réponses possibles : le premier exposant de 2 supérieur à 101 est 128, soit 27, il faut donc un maximum M = 7 essais (26 = 64 serait trop faible).
Insérer un élément dans un tableau. L10.pdf. Download.