

Quantum field theory. Standard Model. Higgs boson. The Higgs boson is named after Peter Higgs, one of six physicists who, in 1964, proposed the mechanism that suggested the existence of such a particle.
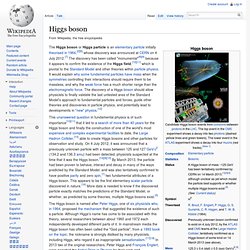
Although Higgs's name has come to be associated with this theory, several researchers between about 1960 and 1972 each independently developed different parts of it. In mainstream media the Higgs boson has often been called the "God particle", from a 1993 book on the topic; the nickname is strongly disliked by many physicists, including Higgs, who regard it as inappropriate sensationalism.[17][18] In 2013 two of the original researchers, Peter Higgs and François Englert, were awarded the Nobel Prize in Physics for their work and prediction[19] (Englert's co-researcher Robert Brout had died in 2011).
A non-technical summary[edit] Theoretical physics. Complex analysis. Murray R.
Spiegel described complex analysis as "one of the most beautiful as well as useful branches of Mathematics". Complex analysis is particularly concerned with the analytic functions of complex variables (or, more generally, meromorphic functions). Because the separate real and imaginary parts of any analytic function must satisfy Laplace's equation, complex analysis is widely applicable to two-dimensional problems in physics. History[edit] Complex logarithm. In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the real natural logarithm ln x is the inverse of the real exponential function ex.
Thus, a logarithm of a complex number z is a complex number w such that ew = z.[1] The notation for such a w is ln z or log z. Since every nonzero complex number z has infinitely many logarithms,[1] care is required to give such notation an unambiguous meaning. If z = reiθ with r > 0 (polar form), then w = ln r + iθ is one logarithm of z; adding integer multiples of 2πi gives all the others.[1] Problems with inverting the complex exponential function[edit] For a function to have an inverse, it must map distinct values to distinct values, i.e., be injective. Euler's formula. This article is about Euler's formula in complex analysis.
For Euler's formula in algebraic topology and polyhedral combinatorics see Euler characteristic. Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Differential equation. Visualization of heat transfer in a pump casing, created by solving the heat equation.
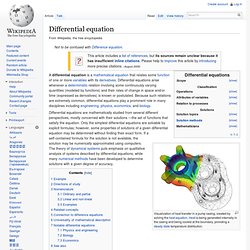
Heat is being generated internally in the casing and being cooled at the boundary, providing a steady state temperature distribution. Differential equations are mathematically studied from several different perspectives, mostly concerned with their solutions —the set of functions that satisfy the equation. Logarithm. The graph of the logarithm to base 2 crosses the x axis (horizontal axis) at 1 and passes through the points with coordinates(2, 1), (4, 2), and (8, 3).
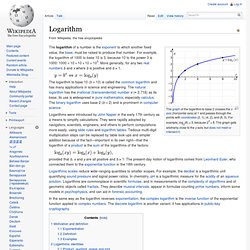
For example, log2(8) = 3, because 23 = 8. The graph gets arbitrarily close to the y axis, but does not meet or intersect it. Physics. Various examples of physical phenomena Physics is one of the oldest academic disciplines, perhaps the oldest through its inclusion of astronomy.[8] Over the last two millennia, physics was a part of natural philosophy along with chemistry, certain branches of mathematics, and biology, but during the Scientific Revolution in the 17th century, the natural sciences emerged as unique research programs in their own right.
[b] Physics intersects with many interdisciplinary areas of research, such as biophysics and quantum chemistry, and the boundaries of physics are not rigidly defined. New ideas in physics often explain the fundamental mechanisms of other sciences[6] while opening new avenues of research in areas such as mathematics and philosophy. Physics also makes significant contributions through advances in new technologies that arise from theoretical breakthroughs. History. Abstract algebra. The permutations of Rubik's Cube have a group structure; the group is a fundamental concept within abstract algebra.
History[edit] As in other parts of mathematics, concrete problems and examples have played important roles in the development of abstract algebra. Through the end of the nineteenth century, many -- perhaps most -- of these problems were in some way related to the theory of algebraic equations. Pi - Numberphile. 1 and Prime Numbers - Numberphile. Problems with Zero - Numberphile. Synesthesia - Numberphile. Topology of a Twisted Torus - Numberphile. Odd Equations - Numberphile. Number Pyramid (very interesting) Integral. Derivative. The graph of a function, drawn in black, and a tangent line to that function, drawn in red. The slope of the tangent line is equal to the derivative of the function at the marked point. The derivative of a function at a chosen input value describes the best linear approximation of the function near that input value. Vector-valued function. Example[edit] A graph of the vector-valued function r(t) = <2 cos t, 4 sin t, t> indicating a range of solutions and the vector when evaluated near t = 19.5 A common example of a vector valued function is one that depends on a single real number parameter t, often representing time, producing a vector v(t) as the result.
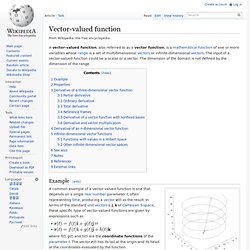
In terms of the standard unit vectors i, j, k of Cartesian 3-space, these specific type of vector-valued functions are given by expressions such as. Parametric equation. For example, the equations Parametric representations are generally nonunique (see the "Examples in two dimensions" section below), so the same quantities may be expressed by a number of different parameterizations.[1] In addition to curves and surfaces, parametric equations can describe manifolds and algebraic varieties of higher dimension, with the number of parameters being equal to the dimension of the manifold or variety, and the number of equations being equal to the dimension of the space in which the manifold or variety is considered (for curves the dimension is one and one parameter is used, for surfaces dimension two and two parameters, etc.).
Parametric equations are commonly used in kinematics, where the trajectory of an object is represented by equations depending on time as the parameter. Applications[edit] Kinematics[edit] Polar coordinate system. Points in the polar coordinate system with pole O and polar axis L. In green, the point with radial coordinate 3 and angular coordinate 60 degrees, or (3,60°). In blue, the point (4,210°). Complex number. Fundamental theorem of algebra. The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root.
This includes polynomials with real coefficients, since every real number is a complex number with zero imaginary part. History[edit] Peter Rothe, in his book Arithmetica Philosophica (published in 1608), wrote that a polynomial equation of degree n (with real coefficients) may have n solutions. Albert Girard, in his book L'invention nouvelle en l'Algèbre (published in 1629), asserted that a polynomial equation of degree n has n solutions, but he did not state that they had to be real numbers. Furthermore, he added that his assertion holds “unless the equation is incomplete”, by which he meant that no coefficient is equal to 0. Mathematics. Mathematics (from Greek μάθημα máthēma, “knowledge, study, learning”) is the study of topics such as quantity (numbers),[2] structure,[3] space,[2] and change.[4][5][6] There is a range of views among mathematicians and philosophers as to the exact scope and definition of mathematics.[7][8] Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements.
Since the pioneering work of Giuseppe Peano (1858–1932), David Hilbert (1862–1943), and others on axiomatic systems in the late 19th century, it has become customary to view mathematical research as establishing truth by rigorous deduction from appropriately chosen axioms and definitions. Mathematics developed at a relatively slow pace until the Renaissance, when mathematical innovations interacting with new scientific discoveries led to a rapid increase in the rate of mathematical discovery that has continued to the present day.[11] History Evolution Etymology. Polynomial.
Power series. Newton's law of universal gravitation. Newton's laws of motion. Modular arithmetic. Group (mathematics) Algebra. "Algebraist" redirects here. For the novel by Iain M. Differential geometry. Quadratic function. Unit Circle. Tensor Calculus Lecture 3: The Covariant Basis. Infinite [Internet Encyclopedia of Philosophy] Euclid. A Way to remember the Entire Unit Circle for Trigonometry. To Infinity And Beyond. Fractals: Hunting The Hidden Dimension.
Infinity is bigger than you think - Numberphile. Transcendental Numbers - Numberphile. Zero Factorial - Numberphile. Riemann Hypothesis - Numberphile. Chaos theory. Introduction to the Line Integral. Introduction to Multivariable Calculus. Number theory. Topology. Calculus. Linear algebra. Riemann Zeta Function.