

KEZAKO: Qu'est ce qu'une fractale? Aux origines leNombre complexe. Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir complexe. L'ensemble des sommes et produits de nombres réels et du nombre imaginaire i (les nombres de la forme a + ib) (en électricité et en électronique, les nombres imaginaires sont identifiés par la lettre j au lieu de i, i étant en électricité et électronique l'intensité du courant) satisfait les propriétés d'une structure de corps commutatif qui contient le corps des réels.
Il est appelé corps des nombres complexes et se note ℂ. Il est muni de l'application module qui généralise la valeur absolue des nombres réels, mais ne peut pas être ordonné totalement de façon compatible avec sa structure de corps. En algèbre, le théorème de d'Alembert-Gauss identifie le degré d'un polynôme complexe non nul au nombre de ses racines comptées avec leur ordre de multiplicité. Pour tenter de comprendre regardez ! Ensemble de Cantor. ENSEMBLE (TRIADIQUE) DE CANTORCantor's (ternary) set, Cantor-(Drittel)Menge L'ensemble (triadique) de Cantor d'extrémité A et B est l'attracteur des deux homothéties de rapport 1/3 et de centres A et B ; en général, on se place dans R avec A = 0 et B = 1 : C est l'attracteur dans R des deux homothéties :

Foutou, Julia & Mandelbrot in english. Louis Pierre Joseph Fatou Pierre Fatou began his studies on mathematics in 1898 at the Ecole Normale Supérieure in Paris. After the exams in 1901 he applied for a job at the observatory in Paris; he thought, that it would be useless to wait for a position as mathematician. He got the job, but nevertheless he continued on his thesis about integration and complex function theory. This having finished 1906, he got his doctorate in 1907. In 1915 the Académie des Sciences published the topic of her "Grand Prix" for 1918. Later it was obvious that these two mathematicians worked on the very same problem going a different way. It seems that Fatou did not really treat fractals, but he prepared basics for the researches of Julia and Mandelbrot. Gaston Maurice Julia. Ensemble Mandelbrot. Benoît Mandelbrot l'art de la rugosité. Mandelbulb 3D délire mathématique. Il y a un mois, on voyait apparaître un peu partout sur internet des images d’une nouvelle famille d’ensembles fractals.
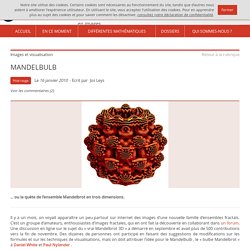
C’est un groupe d’amateurs, enthousiastes d’images fractales, qui en ont fait la découverte en collaborant dans un forum. Une discussion en ligne sur le sujet du « vrai Mandelbrot 3D » a démarré en septembre et avait plus de 500 contributions vers la fin de novembre. Des dizaines de personnes ont participé en faisant des suggestions de modifications sur les formules et sur les techniques de visualisations, mais on doit attribuer l’idée pour le Mandelbulb , le « bulbe Mandelbrot » à Daniel White et Paul Nylander . 2009 formule de White & Nylander. Un article de Wikipédia, l'encyclopédie libre.
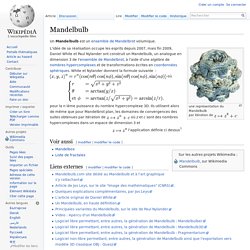
Un Mandelbulb est un ensemble de Mandelbrot volumique. une représentation du Mandelbulb par itération de L'idée de sa réalisation occupe les esprits depuis 2007, mais fin 2009, Daniel White et Paul Nylander ont construit un Mandelbulb, un analogue en dimension 3 de l'ensemble de Mandelbrot, à l'aide d'une algèbre de nombres hypercomplexes et de transformations écrites en coordonnées sphériques.
White et Nylander donnent la formule suivante : où. Paul Nylander’s Web Site. Prise en main Mandelbulb 3D. Paramètres Mandelbulb 3D. Retrouvez mes paramètres Mandelbulb 3D que je mets à disposition du public.
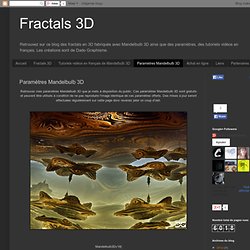
Ces paramètres Mandelbulb 3D sont gratuits et peuvent être utilisés à condition de ne pas reproduire l'image identique de ces paramètres offerts. Des mises à jour seront effectuées régulièrement sur cette page donc revenez jeter un coup d'oeil. Mandelbulb3Dv18{ b......1....7...w....2U...E4d/LPsPDxzmyOIQ4e6PzDWl3RsA33WyHSV.xDNl3xzk/xoZO6ACzj ................................3M9Zp1kZ4/2........Y./..................y.2...wD ...Uz......l4... Tutoriels vidéos in French Mandelbulb 3D. Fractales à tort & à travers. Vous n'y comprenez rien ? Tapez vous la tête contre 1 mur. Jason Padgett. Mandelbrot 1affaire de nombres complexes. L’ensemble de Mandelbrot est une fractale bien connue pour son aspect si particulier en forme de cardioïde : Cet ensemble est défini selon une formule relativement simple que nous verrons plus loin.

Mais comme cette formule fait intervenir les nombres complexes, un petit rappel ne fera pas de mal. Les nombres complexes Si l’on se limite à l’ensemble des nombres réels ( ), il est impossible de calculer la racine carrée d’un nombre négatif, comme par exemple . L’ensemble des nombres complexes () permet de résoudre ce genre de problème. $$\sqrt{-16}=\sqrt(-1\cdot 16)=\sqrt(-1)\cdot\sqrt(16)=i4$$ Quelques spécimens. Fractals Dans cette image, des milliards de mondes...
