

Octonion. In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold .
There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H. The octonions are the largest such algebra, with eight dimensions; twice the number of dimensions of the quaternions, of which they are an extension. They are noncommutative and nonassociative, but satisfy a weaker form of associativity, namely they are alternative. Octonions are not as well known as the quaternions and complex numbers, which are much more widely studied and used.
The octonions were discovered in 1843 by John T. Definition[edit] The octonions can be thought of as octets (or 8-tuples) of real numbers. Where e0 is the scalar or real element; it may be identified with the real number 1. With real coefficients {xi}. Vector space. Vector addition and scalar multiplication: a vector v (blue) is added to another vector w (red, upper illustration).

Below, w is stretched by a factor of 2, yielding the sum v + 2w. An example of a vector space is that of Euclidean vectors, which may be used to represent physical quantities such as forces: any two forces (of the same type) can be added to yield a third, and the multiplication of a force vector by a real multiplier is another force vector. In the same vein, but in a more geometric sense, vectors representing displacements in the plane or in three-dimensional space also form vector spaces. Vectors in vector spaces do not necessarily have to be arrow-like objects as they appear in the mentioned examples: vectors are best thought of as abstract mathematical objects with particular properties, which in some cases can be visualized as arrows.
Introduction and definition[edit] The concept of vector space will first be explained by describing two particular examples: and. Manifold. The surface of the Earth requires (at least) two charts to include every point.
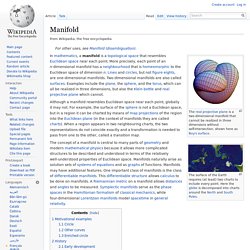
Here the globe is decomposed into charts around the North and South Poles. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows more complicated structures to be described and understood in terms of the relatively well-understood properties of Euclidean space. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. Manifolds may have additional features.
Calabi–Yau manifold. A 2D slice of the 6D Calabi-Yau quintic manifold.
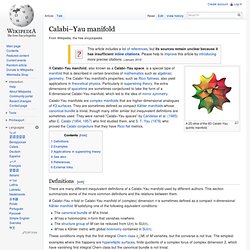
Calabi–Yau manifolds are complex manifolds that are higher-dimensional analogues of K3 surfaces. They are sometimes defined as compact Kähler manifolds whose canonical bundle is trivial, though many other similar but inequivalent definitions are sometimes used. They were named "Calabi–Yau spaces" by Candelas et al. (1985) after E. Calabi (1954, 1957) who first studied them, and S. T. Definitions[edit] There are many different inequivalent definitions of a Calabi–Yau manifold used by different authors. Curse of dimensionality. The curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces (often with hundreds or thousands of dimensions) that do not occur in low-dimensional settings such as the three-dimensional physical space of everyday experience.
The term curse of dimensionality was coined by Richard E. Bellman when considering problems in dynamic optimization.[1][2] Kaluza–Klein theory. This article is about gravitation and electromagnetism.
For the mathematical generalization of K theory, see KK-theory. In 1926, Oskar Klein gave Kaluza's classical 5-dimensional theory a quantum interpretation,[3][4] to accord with the then-recent discoveries of Heisenberg and Schroedinger. Klein introduced the hypothesis that the fifth dimension was curled up and microscopic, to explain the cylinder condition. Klein also calculated a scale for the fifth dimension based on the quantum of charge. It wasn't until the 1940s that the classical theory was completed, and the full field equations including the scalar field were obtained by three independent research groups:[5] Thiry,[6][7][8] working in France on his dissertation under Lichnerowicz; Jordan, Ludwig, and Müller in Germany,[9][10][11][12][13] with critical input from Pauli and Fierz; and Scherrer [14][15][16] working alone in Switzerland.
String theory. String theory was first studied in the late 1960s[3] as a theory of the strong nuclear force before being abandoned in favor of the theory of quantum chromodynamics.
Subsequently, it was realized that the very properties that made string theory unsuitable as a theory of nuclear physics made it a promising candidate for a quantum theory of gravity. Five consistent versions of string theory were developed until it was realized in the mid-1990s that they were different limits of a conjectured single 11-dimensional theory now known as M-theory.[4] Many theoretical physicists, including Stephen Hawking, Edward Witten and Juan Maldacena, believe that string theory is a step towards the correct fundamental description of nature: it accommodates a consistent combination of quantum field theory and general relativity, agrees with insights in quantum gravity (such as the holographic principle and black hole thermodynamics) and has passed many non-trivial checks of its internal consistency.
M-theory. M-theory is a theory in physics that unifies all consistent versions of superstring theory.
The existence of such a theory was first conjectured by Edward Witten at the string theory conference at the University of Southern California in the summer of 1995. Witten's announcement initiated a flurry of research activity known as the second superstring revolution. Background[edit] Quantum gravity and strings[edit]