

Pareto Dominance and Mean Variance. Cardinality. Fractal Geometry. Fractals and Chaos Theory. The picture above is an example of a Julia set.

The picture is a graph of the results of entering a series of numbers into the VERY SIMPLE function f(x) = x2 + c. For this particular graph, the value of c was -0.74 + 0.11i. There are several interesting things about this picture: 1. The image is not the work of a human artist but instead is the result of many repetitions of a simple mathematical calculation - and yet the image contains infinite complexity and a clear aesthetic quality. 2. 3. Below is an animation which shows the result of zooming in and out on the Mandlebrot set. The following are Java Applets that generate fractals: The first Java Applet is in color and allows you to zoom in on regions of the complex plane.
Click Here for a Mandelbrot Set generator. Below are simple Java Applets that generate both Mandelbrot and Julia Sets - the code is included with each because they are short and simple enough to be understood with a minimum of programming knowledge. Definitons: 1. 2. 3. Laplace operator. The Laplace operator is named after the French mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics, where the operator gives a constant multiple of the mass density when it is applied to a given gravitational potential.
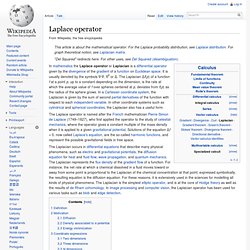
Solutions of the equation ∆f = 0, now called Laplace's equation, are the so-called harmonic functions, and represent the possible gravitational fields in free space. The Laplacian occurs in differential equations that describe many physical phenomena, such as electric and gravitational potentials, the diffusion equation for heat and fluid flow, wave propagation, and quantum mechanics. The Laplacian represents the flux density of the gradient flow of a function. Definition[edit]
Ordinal number. Representation of the ordinal numbers up to ωω.
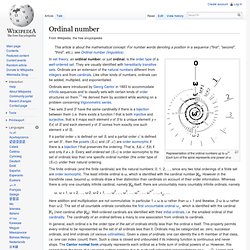
Each turn of the spiral represents one power of ω In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals. Like other kinds of numbers, ordinals can be added, multiplied, and exponentiated.
Ordinals were introduced by Georg Cantor in 1883 to accommodate infinite sequences and to classify sets with certain kinds of order structures on them.[1] He derived them by accident while working on a problem concerning trigonometric series. Two sets S and S' have the same cardinality if there is a bijection between them (i.e. there exists a function f that is both injective and surjective, that is it maps each element x of S to a unique element y = f(x) of S' and each element y of S' comes from exactly one such element x of S). . (next cardinal after ). General Systems Theory. © 1993, David S.

Walonick, Ph.D. General systems theory was originally proposed by biologist Ludwig von Bertalanffy in 1928. Since Descartes, the "scientific method" had progressed under two related assumptions. A system could be broken down into its individual components so that each component could be analyzed as an independent entity, and the components could be added in a linear fashion to describe the totality of the system. Von Bertalanffy proposed that both assumptions were wrong.
One common element of all systems is described by Kuhn. Systems can be either controlled (cybernetic) or uncontrolled. Stochastic process. Stock market fluctuations have been modeled by stochastic processes.
In probability theory, a stochastic process /stoʊˈkæstɪk/, or sometimes random process (widely used) is a collection of random variables; this is often used to represent the evolution of some random value, or system, over time. This is the probabilistic counterpart to a deterministic process (or deterministic system). Instead of describing a process which can only evolve in one way (as in the case, for example, of solutions of an ordinary differential equation), in a stochastic or random process there is some indeterminacy: even if the initial condition (or starting point) is known, there are several (often infinitely many) directions in which the process may evolve.
Formal definition and basic properties[edit] Definition[edit] Riemannian manifold. In differential geometry, a (smooth) Riemannian manifold or (smooth) Riemannian space (M,g) is a real smooth manifold M equipped with an inner product on the tangent space at each point that varies smoothly from point to point in the sense that if X and Y are vector fields on M, then.

Barc. Nonlinear Geoscience (Fractals) Let's Generate Fractals A simple artificial self-similar form that has been closely studied for a long time is Koch curve (named after Swedish mathematician Helge von Koch).
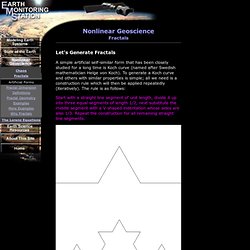
To generate a Koch curve and others with similar properties is simple; all we need is a construction rule which will then be applied repeatedly (iteratively). The rule is as follows: Start with a straight line segment of unit length, divide it up into three equal segments of length 1/2, next substitute the middle segment with a V-shaped indentation whose sides are also 1/3. Repeat the construction for all remaining straight line segments. Fractal Markets.