

Phi. Cette page contient des caractères spéciaux ou non latins.
Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation…), consultez la page d’aide Unicode. Ne doit pas être confondu avec pHi, Փ ou ɸ. Caractéristiques[modifier | modifier le code] Usage[modifier | modifier le code] En grec ancien, le phi se prononce vraisemblablement [pʰ], puis évolue vers [ɸ]. Dans le système de numération grecque, phi vaut 500 ; par exemple ‹ φʹ › représente le nombre 500. Comme la plupart des autres lettres grecques, le phi est parfois utilisé en dehors de son contexte alphabétique grec dans les sciences. Nom[modifier | modifier le code] En grec, la lettre est appelée φι (fi), prononcée /fi/. En grec ancien, elle est appelée φῖ[1] (fî), prononcée en attique /ˈpʰiːˌ/, ou φεῖ[2] (feî), prononcée /ˈpʰeː/.
Typographie[modifier | modifier le code] La forme bas-de-casse du phi possède deux variantes typographiques, héritées de l'écriture manuscrite médiévale. Le nombre d'or - Micmaths. Identité remarquable. Représentation graphique de l'identité remarquable Identités remarquables du second degré[modifier | modifier le code] Dans toute la suite, a et b désignent des nombres, qui peuvent être des entiers, des rationnels et réels, ou même des complexes.
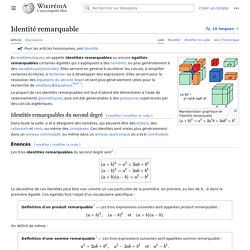
Ces identités sont vraies plus généralement dans un anneau commutatif, ou même dans un anneau quelconque où a et b commutent. Énoncés[modifier | modifier le code] Les trois identités remarquables du second degré sont[1] : La deuxième de ces identités peut être vue comme un cas particulier de la première, en prenant, au lieu de b, –b dans la première égalité. Définition d'un produit remarquable[1] — Les trois expressions suivantes sont appelées produit remarquable : On définit de même : Définition d'une somme remarquable[1] — Les trois expressions suivantes sont appelées somme remarquable : Nombre d'or. La proportion définie par a et b est dite d'« extrême et moyenne raison » lorsque a est à b ce que a + b est à a, soit : lorsque (a + b)/a = a/b.
Le rapport a/b est alors égal au nombre d'or. Le nombre d'or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b), ce qui s'écrit : Le découpage d'un segment en deux longueurs vérifiant cette propriété est appelé par Euclide découpage en « extrême et moyenne raison ». Le nombre d'or est maintenant souvent désigné par la lettre φ (phi), et il est lié à l'angle d'or. Ce nombre irrationnel est l'unique solution positive de l'équation x2 = x + 1. Équation du second degré. Sur le corps des nombres complexes, une équation du second degré a toujours exactement deux racines distinctes ou une racine double.

Dans l'algèbre des quaternions, une équation du second degré peut avoir une infinité de solutions. Historique[modifier | modifier le code] Les équations du second degré sont au centre de l'algèbre babylonienne, dès avant le XVIIIe siècle av. J. -C.[1]. Au VIIIe siècle, le mathématicien indien Sridhar Acharya (en) indique la manière de calculer les deux racines réelles. Les équations du second degré ont été étudiées systématiquement par Al-Khwarizmi au IXe siècle, dans un ouvrage intitulé Abrégé du calcul par la restauration et la comparaison qui, via le mot « restauration » (en arabe : al-jabr) a donné son nom à l'algèbre.
Il démontre les méthodes de résolution en suivant des raisonnements d'algèbre géométrique. Éléments clé[modifier | modifier le code] Introduction par l'exemple[modifier | modifier le code] .