

Fibonacci Lemonade. How would one make mathematical cuisine?
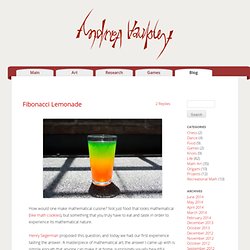
Not just food that looks mathematical (like math cookies), but something that you truly have to eat and taste in order to experience its mathematical nature. Henry Segerman proposed this question, and today we had our first experience tasting the answer. A masterpiece of mathematical art, the answer I came up with is simple enough that anyone can make it at home, surprisingly visually beautiful, delicious… Layered Drinks! Not just any layered drinks, of course. Additionally, the ratio of sugar to lemon juice in our lemonade isn’t constant. Layer 3 is 1 part lemon, 1 part sugar. Generically, for layer n > 2, there are fib(n-1) parts sugar and fib(n-2) parts lemon juice. Surprisingly, using golden ratio relative proportions of lemon juice and simple syrup actually seems to make rather good lemonade.
You too can make Fibonacci lemonade and experience the taste of exponential flavor, the golden ratio, and the Fibonacci sequence. The Method. Math Circle – Celtic Knots. Math Circle – Halving Fun. I recently led a recreational session at (MC)^2—that’s the Mercer County Math Circle.

I called the session “Halving Fun”. I don’t remember exactly how I hit upon halving—maybe because of a partition puzzle I’ve been contemplating—but I knew I was excited to share how much great mathematics can come from such a seemingly simple concept. Here’s the session description: Join us as we “halve” some fun while creating some art and solving some puzzles that involve breaking shapes in half.
What’s the most beautiful way you could cut a square into two equal pieces? Shell Centre for Mathematical Education Publications Ltd. This particular 'cluster book', FINDING OUT, offers a range of materials designed to support students as they pursue extended tasks relating to statistical investigations.
The material has been designed and tested, as extended tasks, in a range of classrooms. A total of about twelve to fifteen hours study time, usually over a period of two to three weeks, was spent on each task. Many of the ideas have been used to stimulate work for a longer period of time than this, but any period which is significantly shorter has proved to be rather unsatisfactory. The lead task in this book is called Why Are We Waiting? It is based upon real life experiences, and provides a rich and tractable environment for extended tasks. Unless stated otherwise, these materials are Copyright © Shell Centre for Mathematical Education (see the materials for full details). Pseudocontext Saturdays: Introduction. September 18th, 2010 by Dan Meyer 2013 Jun 26.
Other People’s Problems. October 27th, 2011 by Dan Meyer Malcolm Swan: Draw a shape on squared paper and plot a point to show its perimeter and area.
Which points on the grid represent squares, rectangles, etc. Draw a shape that may be represented by the point (4, 12) or (12, 4). Find all the “impossible” points. I like this problem a lot (I’ll spoil some of the fun in the comments) even though it’s fundamentally dissimilar to most of the problems I write about here. One of the best parts about my working life right now, including grad school and my work with publishers, is my daily exposure to the vast set of answers to the question, “What makes for good math education?” So I’m grateful to instructors like Labaree and Stevens who urged us all to quit trying to solve the problem and focus first on describing the domain of the problem and its range of solutions. What makes a good problem?
Let's start things off with a short taxonomy of problems: 1.

Valuable problems are problems that worth doing. You'll learn something from engaging and eventually solving them. 2. Hooky problems are problems that keep you up at night. They aren't boring -- they're what you do when other things are boring. The Space Between the Numbers. This may be the single most important question a teacher—in any subject—learns to ask him/herself.

I am, for obvious reasons, more familiar with talking about how this pertains to math problems. Perhaps then, I am mistaken when I say that I believe there is a special aspect to finding good math problems that is not present in other disciplines. Without Geometry, Life is Pointless: What Makes a Problem Great. I've put together an ever evolving list of characteristics of rich math problems.
Anything you'd add, subtract, or edit? These are in no particular order... 1. The problem should be accessible. A Critical Language for Problem Design «Research in Practice Research in Practice. I am at the Joint Mathematics Meetings this week.
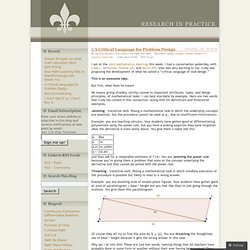
I had a conversation yesterday, with Cody L. Patterson, Yvonne Lai, and Aaron Hill, that was very exciting to me. Cody was proposing the development of what he called a “critical language of task design.” This is an awesome idea. But first, what does he mean? He means giving (frankly, catchy) names to important attributes, types, and design principles, of mathematical tasks. Jamming – transitive verb.