

Variété (géométrie) Un article de Wikipédia, l'encyclopédie libre.
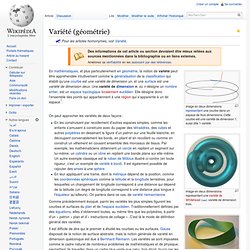
Pour les articles homonymes, voir Variété. Image en deux dimensions représentant une courbe dans un espace de trois dimensions. Cette courbe est une variété de dimension 1, aussi dite 1-variété. Réalisation du ruban de Möbius à partir du collage d'une bande de papier. Le « bord » n'est que d'un seul tenant. On peut approcher les variétés de deux façons : Il est difficile de dire qui le premier a étudié les courbes ou les surfaces. La topologie algébrique cherche à classer les variétés (mais aussi des objets plus généraux) en en déterminant des invariants, c'est-à-dire des objets mathématiques — qui peuvent être des nombres réels — associés à chaque variété et qui en caractérisent la topologie.
Les variétés constituent à la fois un cadre et un sujet d'étude communs pour les chercheurs en mathématiques et en physique. Portail:Géométrie. Catégorie:Géométrie. Pourquoi la Géométrie ? Un exemple élémentaire. Nous avons vu que la géométrie était la grande victime des nouveaux programmes du Lycée, et bientôt des prépas.
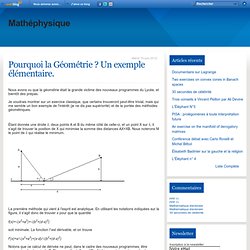
Je voudrais montrer sur un exercice classique, que certains trouveront peut-être trivial, mais qui me semble un bon exemple de l'intérêt (je ne dis pas supériorité) et de la portée des méthodes géométriques. Étant donnée une droite δ, deux points A et B du même côté de celle-ci, et un point X sur δ, il s'agit de trouver la position de X qui minimise la somme des distances AX+XB. Nous noterons M le point de δ qui réalise le minimum. La première méthode qui vient à l'esprit est analytique. En utilisant les notations indiquées sur la figure, il s'agit donc de trouver x pour que la quantité.
Transformations géométriques. La dualité de Poincaré. Il sera question dans cet article d’une nouvelle forme de calcul développée par Henri Poincaré à partir de 1895, portant sur les figures vivant dans les espaces de dimension quelconque.
Elle lui permit de définir des mesures numériques de la forme de ces espaces, leurs nombres de Betti. Lorsque l’espace est refermé sur lui-même comme une surface sphérique, ces nombres vérifient une étonnante propriété de symétrie, qui porte depuis le nom de dualité de Poincaré. Poincaré en proposa deux stratégies de preuve. Nous décrirons ces stratégies, ainsi que les nouvelles mesures de la forme des espaces découvertes par Poincaré lorsqu’il méditait sur la deuxième d’entre elles. Nous examinerons enfin quelques travaux précurseurs, afin de mieux mettre en évidence l’apport de Poincaré. De l’espace unique à la pluralité des espaces.
Géométrie Différentielle. Géométrie Spectrale. Groupe de Géométrie. Cercle - angles. Dans un polygone régulier, les côtés sont égaux (de même longueur) Les arcs interceptés sont égaux également.

Les angles au centre interceptant des arcs égaux, sont égaux Dans cet hexagone, il y a six angles aux entre qui couvrent 360°. Chacun mesure 360/6 = 60°. Euclid's Elements, Table of Contents. The first six books of the Elements of Euclid, ... Euclide d'Alexandrie. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges On ne possède pas d'informations précises sur la vie d'Euclide et sur la période précise où il vécut.

Il semble avoir été dans la force de l'âge vers -285 avant J. -C., qu'il étudia à Athènes à l'École des successeurs de Platon et qu'il s'établit à Alexandrie, sur l'invitation de Ptolémée II, roi d'Égypte, où Apollonius fut un de ses élèves. ➔ Le nom d'Euclide se rattache à de nombreux concepts mathématiques, il s'agit cependant d'éviter tout anachronisme. Des appellations comme : distance euclidienne, espace vectoriel euclidien, espace localement euclidien, norme euclidienne, veulent rappeler que le contexte mathématique sous-jacent est compatible avec la géométrie élémentaire de ce grand (immense, génial) mathématicien. »Plan euclidien , distance , norme , espaces topologiques. Théorème de Ceva. Un article de Wikipédia, l'encyclopédie libre.
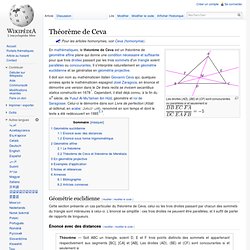
Les droites (AD), (BE) et (CF) sont concourantes ou parallèles si et seulement si Il doit son nom au mathématicien italien Giovanni Ceva qui, quelques années après le mathématicien espagnol José Zaragoza, en énonce et démontre une version dans le De lineis rectis se invicem secantibus statica constructio en 1678[1]. Cependant, il était déjà connu, à la fin du XIe siècle, de Yusuf Al-Mu'taman ibn Hűd, géomètre et roi de Saragosse. Celui-ci le démontre dans son Livre de perfection (Kitab al-Istikmal, en arabe: كتاب الإستكمال), renommé en son temps et dont le texte a été redécouvert en 1985[2],[3]. Géométrie euclidienne[modifier | modifier le code] Cette section présente un cas particulier du théorème de Ceva, celui où les trois droites passant par chacun des sommets du triangle sont intérieures à celui-ci. Énoncé avec des distances[modifier | modifier le code] Démonstration — On note dans la suite. Théorème de Morley. Un article de Wikipédia, l'encyclopédie libre.
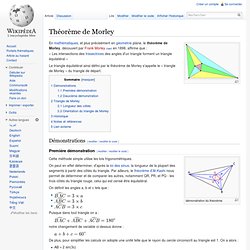
En mathématiques, et plus précisément en géométrie plane, le théorème de Morley, découvert par Frank Morley (en) en 1898, affirme que :« Les intersections des trissectrices des angles d'un triangle forment un triangle équilatéral » Le triangle équilatéral ainsi défini par le théorème de Morley s'appelle le « triangle de Morley » du triangle de départ. Démonstrations[modifier | modifier le code] Première démonstration[modifier | modifier le code] démonstration du théorème Cette méthode simple utilise les lois trigonométriques. On peut en effet déterminer, d'après la loi des sinus, la longueur de la plupart des segments à partir des côtés du triangle. On définit les angles a, b et c tels que : Topologie.