

Page pour le téléchargement de la brochure : Autour de Thalès - Le portail des IREM. Gèomètrie. Présentation TIC. Paper Snowflake Maker. Mémoire de CAFIPEMF Géraldine.doc - memCAFIPEMFcabri.pdf. Microsoft Word - COURS 6c LA RÈGLE CRAS.doc - cras. Microsoft Word - DDM-Geo.doc - DDM-Geo.pdf. Microsoft Word - DDM-Geo.doc - DDM-Geo.pdf. Figures à réaliser au compas ou dans un repère. Geometry Géométrie Geometria - Accueil. 2012-06-08-CS-IREM - Annexe_3. Afficher le sujet - la perspective by Chaos. Article de Chaos Factory Il ne s'agit pas absolument pas ici d'un cours magistral, mais d'une rapide révision des bases, des trucs et astuces, qui nous permettent de prendre plus de liberté avec la terrible perspective.
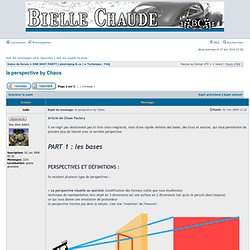
PART 1 : les bases Ils existent plusieurs type de perspectives : • La perspective visuelle ou spatiale (modification des formes) (celle que nous étudierons)technique de représentation d'un objet en 3 dimensions sur une surface en 2 dimensions (tel qu'on le perçoit dans l'espace)ce qui nous donne une simulation de profondeurla perspective n'existe pas dans la nature, c'est une "invention" de l'homme". Nouvelle page 1. - reconnaître, décrire et nommer les figures et solides usuels. - utiliser la règle, l’équerre et le compas pour vérifier la nature de figures planes usuelles et les construire avec soin et précision - savoir organiser des informations numériques ou géométriques, justifier et apprécier la vraisemblance d’un résultat (Horaires et programmes de l’enseignement primaire, cycle 3, BO hors-série n°3 du 19 juin 2008) Les programmes du cycle 2 précisent que : « Les élèves enrichissent leurs connaissances en matière d’orientation et de repérage.

. « Certaines figures planes sont reconnues globalement de façon perceptive par les élèves. Les figures utilisées doivent être de différentes tailles, présentées dans des positions variées, notamment en travaillant avec des figures découpées que l’élève peut manipuler. Source : Documents d’application des programmes mathématiques, cycle 2, collection « École » CNDP Paris 2002.
Activités mathématiques. Les activités au collège. Dans nos classes - Des polygones et des angles en cinquième. Par Michèle Drouilhet et Laurence Konilovski [1] Introduction Habituellement pour introduire la propriété de la somme des angles d’un triangle, on commence par conjecturer soit par découpage soit par mesure, puis on démontre cette conjecture en utilisant la notion d’angles alternes-internes et en introduisant la droite passant par un sommet du triangle et parallèle au côté opposé.

L’introduction de cette droite nous a toujours semblée artificielle et nous nous sommes alors posé la question de trouver une approche plus naturelle pour les élèves. Cette réflexion a été proposée lors de réunions de formation de formateurs associés au stage du PAF intitulé « Démonstrations au collège ». Matlet. Une sélection de programmes à utiliser en ligne.
Les applets ont été développées par le Freudenthal Institut Researchgroup in Mathematics education d'Utrecht, aux Pays-Bas, au cours de nombreuses années de recherche et d'expérimentation. Aujourd'hui, quelques-unes de ces applets sont mises à disposition des écoles suisses grâce à la disponibilité de l'Institut hollandais et au projet commun du Centre fri-tic du canton de Fribourg, du Centro didattico du canton du Tessin et de ICT Basler Schulen du canton de Bâle.
Chacune des applets est accompagnée d'une brève description et d'un feuille de route didactique détaillée. Ces commentaires ont été mis à jour en juin 2011 pour être en accord avec le Plan d'études romand ainsi que pour respecter la désignation HarmoS des années scolaires de 1 (préscolaire) à 11 (dernière année d'école obligatoire).
Les applets peuvent être utilisées librement. Les applets sont programmées en langage Java. Matlet. Aide_perso_geometrie_C3.pdf (Objet application/pdf) Robert_caroline.pdf (Objet application/pdf) Généralités. Les nombres entiers font immédiatement penser à la suite 1,2,3,4,5,...
Une suite que tout élève va apprendre à dire, à écrire, à utiliser: Papiers-Crayons avec GeoGebra. Papiers Crayons avec Geogebra (ou DGPad) Les fichiers GeoGebra suivants sont inspirés de la brochure "Papiers-Crayons" de l’IREM Paris-Nord.
Le principe pédagogique et le cadre d’utilisation de ces activités sont décrits dans le chapitre "lignes droites" de l’article "Géométrie plane au cycle 3" : suivre ce lien pour y accéder. Tous les fichiers de cet article sont aussi accessibles sur Rubricamaths, le site d’activités informatiques de l’IREM. L’accès aux activités y est plus aisé pour travailler avec les élèves} Les différentes activités proposées dans le livre Sommaire :
3DMAVR10.pdf (Objet application/pdf) Géométrie, mesurer la terre, mesurer la Terre ? Géométrie.
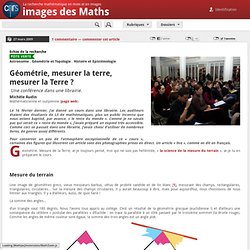
Mesure de la Terre, ai-je toujours pensé, moi qui ne suis pas helléniste, « la science de la mesure du terrain », ai-je lu en préparant le cours. Mesure du terrain Une image de géomètres grecs, vieux messieurs barbus, vêtus de probité candide et de lin blanc [1], mesurant des champs, rectangulaires, triangulaires, circulaires... Sur la mesure des champs circulaires, il y aurait beaucoup à dire, mais pour aujourd’hui, nous choisissons de nous limiter aux triangles.
Il y a d’ailleurs, aussi, de quoi faire ! Geometría. ¿Quien iba a imaginar que podía haber otros tipos de paralelas?
Durante siglos sólo se concebía la geometría euclídea, pero el tesón de los matemáticos¹ por encontrar explicaciones convincentes llevó a superar el 5º postulado de los Elementos y abrir nuevos mundos. Euclides fue superado, pero sigue siendo válido y es bien honrado, muchas mates llevan su nombre. Foto Eckhart Pedersen.¹En matemáticas no importa estar siglos sin solución, se puede decir no lo sabemos, es mejor pensar con libertad que aceptar falsedades. Circunferencia es lo de fuera, la línea que rodea el círculo, que es lo de dentro, la superficie total.
MATHCURVE.COM. Pythagore - Wolfram demonstartion projet - Search Results - pythagoras.