

Homologie et Topologie - Master 2 Math (Lille 1) (Dernière mise à jour : 15/12/2014) NOUVEAU : vidéos des cours 11 et 12 Cours fondamental du Master Mathématiques Recherche, 2ième année, Semestre 3 (2014-15) - Université Lille 1 par Ivo Dell'Ambrogio et Benoit Fresse Présentation | Plan du cours | Prérequis et bibliographie | Fiches TD | Vidéos | Exposés de séminaire | Mémoires de M2 | Informations pratiques Présentation Le but de ce cours sera d'introduire des concepts et des outils fondamentaux de topologie algébrique.

Ce cours permettra d'aborder le cours proposé par Alexis Virelizier sur les théories des champs quantiques topologiques au second semestre. On partira de questions classiques (triangulation des surfaces, des variétés), puis on introduira la théorie de l'homologie singulière qui nous permettra de prouver l'invariance topologique d'expressions combinatoires introduites en première partie.
Plan du cours. Plan cours 2013 2014. Cours topoalg. Lexique. Glossaire de topologie. Vocabulaire général. Topologie générale. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Les progrès de l'analyse, dans l'étude des fonctions continues (naïvement : dont la représentation graphique n'a pas de trous), de leur dérivabilité, de leurs limites en un point (fini ou non), de l'existence d'extremums, demandaient une définition rigoureuse de l'idée intuitive de proximité, tout particulièrement lors d'opérations sur ces fonctions.

Les suites de fonctions et la "découverte" de la convergence uniforme nécessitèrent de nouveaux outils. Espace topologique. Les espaces topologiques forment le socle conceptuel permettant de définir ces notions. Elles sont suffisamment générales pour s'appliquer à un grand nombre de situations différentes : ensembles finis, ensembles discrets, espaces de la géométrie euclidienne, espaces numériques à n dimensions, espaces fonctionnels plus complexes, mais aussi en géométrie algébrique. Ces concepts apparaissent dans presque toutes les branches des mathématiques ; ils sont donc centraux dans la vision moderne des mathématiques. La topologie générale définit le vocabulaire fondamental, mais permet aussi la démonstration de résultats non triviaux et puissants, tels que le théorème de Baire. Quelques notions de topologie. En économie, les problèmes d’optimisation et notamment ceux qui se fondent sur l’utilisation de fonctions à deux variables requièrent un certain bagage mathématique.

Celui-ci comprend des notions de topologie, notamment pour reconnaître la nature des ensembles de définition. Certaines de ces notions sont assez simples à saisir et sont connues par les lycéens (sans toutefois qu’ils fassent le lien avec des concepts qu’ils découvriront pour certains à bac + 3). D’autres sont beaucoup plus difficiles à saisir intellectuellement.
Cette page, l’une des plus abstraites proposées par ce site web, est une introduction à ces notions aux noms parfois étranges… La topologie est une branche des mathématiques qui étudie les déformations indépendamment des grandeurs. « La géométrie s'intéresse à des notions comme la position absolue d'un point, la distance ou le parallélisme, qui changent avec la forme de l'espace considéré. Ainsi, la théorie des graphes est étroitement liée à la topologie. Topologie des espaces normés.
Homotopie. Intérieur (topologie) Adhérence. Ouvert (topologie) Il existe plusieurs définitions des ouverts suivant le type d'espace concerné.
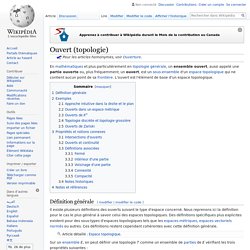
Nous reprenons ici la définition pour le cas le plus général à savoir celui des espaces topologiques. Des définitions spécifiques plus explicites existent pour des sous-types d'espaces topologiques tels que les espaces métriques, espaces vectoriels normés ou autres. Ces définitions restent cependant cohérentes avec cette définition générale. Frontière (topologie) Un article de Wikipédia, l'encyclopédie libre. En topologie, la frontière d'un ensemble est constituée des points qui, de façon intuitive, sont « situés au bord » de cet ensemble, c’est-à-dire qui peuvent être « approchés » à la fois par l'intérieur et l'extérieur de cet ensemble. Il est possible de définir la frontière de S (souvent notée ∂S ou Fr S) de plusieurs façons équivalentes : Continuité (mathématiques) Un article de Wikipédia, l'encyclopédie libre.
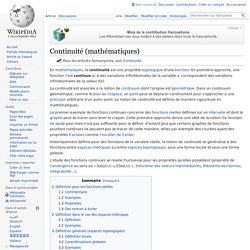
Historiquement définie pour des fonctions de la variable réelle, la notion de continuité se généralise à des fonctions entre espaces métriques ou entre espaces topologiques, sous une forme locale et sous une forme globale. L'étude des fonctions continues se révèle fructueuse pour les propriétés qu'elles possèdent (propriété de convergence au sens où « lim(f(x)) = f(lim(x)) », théorème des valeurs intermédiaires, théorème des bornes, intégrabilité…). une fonction définie sur I à valeurs réelles et La fonction f est dite continue en a si : Fonction continue nulle part dérivable. Un article de Wikipédia, l'encyclopédie libre.
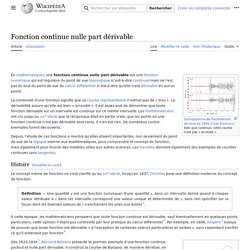
La continuité d'une fonction signifie que sa courbe représentative n'admet pas de « cassure ». La dérivabilité assure qu'elle est bien « arrondie ». Il est assez aisé de démontrer que toute fonction dérivable sur un intervalle est continue sur ce même intervalle. Les mathématiciens ont cru jusqu'au XIXe siècle que la réciproque était en partie vraie, que les points où une fonction continue n'est pas dérivable sont rares. Il n'en est rien. Histoire[modifier | modifier le code] Variété. VARIÉTÉVariety (or manifold), Varietät (oder Mannigfaltigkeit) Une variété topologique de dimension n est un espace topologique localement homéomorphe à l'espace euclidien de dimension n ou au demi-espace (i.e. dont tout point possède un voisinage homéomorphe à ou Les points ayant un voisinage homéomorphe au demi-espace forment le "bord" de la surface ; une variété sans bord est dite simple.

Variété (géométrie) Pour les articles homonymes, voir Variété. Image en deux dimensions représentant une courbe dans un espace de trois dimensions. Plongement. Un article de Wikipédia, l'encyclopédie libre.
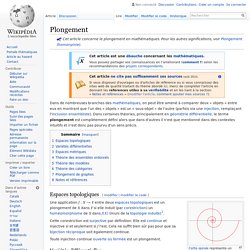
Espaces topologiques[modifier | modifier le code] Toute injection continue ouverte ou fermée est un plongement. Variétés différentielles[modifier | modifier le code] En topologie différentielle, soient V et W deux variétés de classe Ck (éventuellement k infini), et f : V → W une fonction. On dit que f est un plongement Ck si c'est un plongement au sens topologique et si, de plus, f est Ck et pour tout x∈V, l'application linéaire tangente Tf(x) est injective. Compacité (mathématiques) Un article de Wikipédia, l'encyclopédie libre.
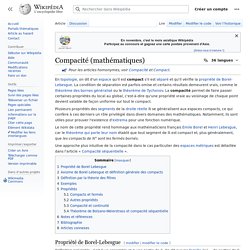
Une approche plus intuitive de la compacité dans le cas particulier des espaces métriques est détaillée dans l'article « Compacité séquentielle ». Pour une démonstration de cette propriété voir le théorème de Borel-Lebesgue, aussi appelé théorème de Heine-Borel. Un espace topologique E est dit quasi-compact s'il vérifie l'axiome de Borel-Lebesgue : de tout recouvrement ouvert de E, on peut extraire un sous-recouvrement fini. L'espace est dit compact quand il est en outre séparé au sens de Hausdorff (T2). Espace contractile. Un article de Wikipédia, l'encyclopédie libre.
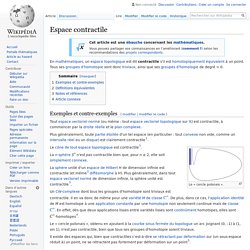
En mathématiques, un espace topologique est dit contractile s'il est homotopiquement équivalent à un point. Tous ses groupes d'homotopie sont donc triviaux, ainsi que ses groupes d'homologie de degré > 0. Exemples et contre-exemples[modifier | modifier le code] Tout espace vectoriel normé (ou même : tout espace vectoriel topologique sur ℝ) est contractile, à commencer par la droite réelle et le plan complexe. La n-sphère Sn n'est pas contractile bien que, pour n ≥ 2, elle soit simplement connexe. Topologie quotient. En mathématiques, la topologie quotient consiste intuitivement à créer une topologie en collant certains points d'un espace donné sur d'autres, par le biais d'une relation d'équivalence bien choisie.
Cela est souvent fait dans le but de construire de nouveaux espaces à partir d'anciens. On parle alors d'espace topologique quotient. Motivations[modifier | modifier le code] Beaucoup d'espaces intéressants, le cercle, les tores, le ruban de Möbius, les espaces projectifs sont définis comme des quotients. La topologie quotient fournit souvent la façon la plus naturelle de munir un ensemble défini « géométriquement » d'une topologie naturelle.
Citons aussi le cas des surfaces de ℝ3 particulières : les tores à Définition et principales propriétés[modifier | modifier le code] Topologie de la droite réelle. Théorème du point fixe de Brouwer. Chemin (topologie) Un article de Wikipédia, l'encyclopédie libre. Points parcourus par un chemin de A à B dans R². Cependant, différents chemins peuvent parcourir le même ensemble de points. f : I → X. Le point initial du chemin est f(0) et le point final est f(1). On parle souvent de « chemin reliant x à y » où x et y sont les points initiaux et finaux du chemin. Topologie - Boules. Topologie - Ouverts et Fermés. Topologie - Adhérence et Intérieur. Un plongement d'une surface dans R3 est une représentation où le plan tangent est continu et où il n'existe aucun ensemble d'auto-intersection. Conjecture de Poincaré : les révélations de Perelman. Jean-Pierre Petit - LE TOPOLOGICON.
Topologie - 4e ed. - Cours et exercices corrigés - Hervé Queffélec. Topologie générale: Chapitres 1 à 4 - N. Bourbaki. Experiments in Topology - Stephen Barr. Abdelhaq El Jai - élements de topologie et espaces métriques. Topologie sa petite enfance. Topologie algebrique. Mohammed BOUAYAD - PRETOPOLOGIE ET RECONNAISSANCES DES FORMES (thèse) Elements of Combinatorial and Differential Topology - Viktor Vasilʹevich Prasolov.