Mathematics
Get flash to fully experience Pearltrees
Math for Artists: Exponents and Radicals
Math for Artists: Exponents and Radicals by Theresa L. Ford, 9-17-2004 Back to my School Stuff Math for Artists - Now a multi-touch, interactive book for iPad® .
Blog : Test Your “Subitizing” Ability
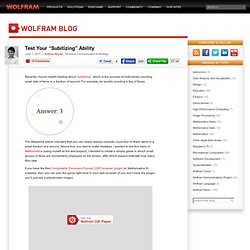
Recently I found myself reading about “ subitizing ”, which is the process of instinctively counting small sets of items in a fraction of second. For example, try quickly counting a few of these: The Wikipedia article indicates that you can nearly always correctly count four or fewer items in a small fraction of a second. Above four, you start to make mistakes.
Nerd Paradise : Divisibility Rules for Arbitrary Divisors
It's rather obvious when a number is divisible by 2 or 5, and some of you probably know how to tell if a number is divisible by 3, but it is possible to figure out the division 'rule' for any number. Here are the rules for 2 through 11... The last digit is divisible by 2.
We can find interactive sites on the internet (like this ) to draw points, move them, and check how the structure becomes updated in real time. In fact, if we have a series of random dots scattered in the plane, the best way of finding the correct Voronoi Telesación for this set is using the Delaunay triangulation. And in fact, this is precisely the idea shown on the animation: first the Delaunay Triangulation and then, subsequently, the Voronoi Tessellation . But to draw a correct Delaunay Triangulation is necessary to meet the so-called “Delaunay Condition”. This means that: a network of triangles could be considered Delaunay Triangulation if all circumcircles of all triangles of the network are “empty”. Notice that actually, given a certain number of points in the plane there is no single way to draw triangles, there are many.
Nature by numbers. The theory behind this movie
Free Mathematics Books
Here is an alphabetical list of online mathematics books, textbooks, monographs, lecture notes, and other mathematics related documents freely available on the web. I tried to select only the works in book formats, "real" books that are mainly in PDF format, so many well-known html-based mathematics web pages and online tutorials are left out. Click here if you prefer a categorized directory of mathematics books . The list is updated almost on a daily basis, so, if you want to bookmark this page, use the button in the upper right corner. 001. Noncompact Harmonic Manifolds Gerhard Knieper, Norbert Peyerimhoff | arXiv Published in 2013, 84 pages
This page has been split into TWO PARTS. This, the first , looks at the Fibonacci numbers and why they appear in various "family trees" and patterns of spirals of leaves and seeds. The second page then examines why the golden section is used by nature in some detail, including animations of growing plants. Let's look first at the Rabbit Puzzle that Fibonacci wrote about and then at two adaptations of it to make it more realistic. This introduces you to the Fibonacci Number series and the simple definition of the whole never-ending series. Fibonacci's Rabbits
The Fibonacci Numbers and Golden section in Nature - 1
The above two figures are rearrangements of each other, with the corresponding triangles and polyominoes having the same areas. Nevertheless, the bottom figure has an area one unit larger than the top figure (as indicated by the grid square containing the dot). The source of this apparent paradox is that the "hypotenuse" of the overall "triangle" is not a straight line, but consists of two broken segments. As a result, the "hypotenuse" of the top figure is slightly bent in, whereas the "hypotenuse" of the bottom figure is slightly bent out. The difference in the areas of these figures is then exactly the "extra" one unit.
Triangle Dissection Paradox
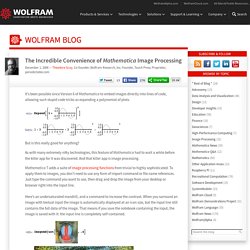
It’s been possible since Version 6 of Mathematica to embed images directly into lines of code, allowing such stupid code tricks as expanding a polynomial of plots. But is this really good for anything? As with many extremely nifty technologies, this feature of Mathematica had to wait a while before the killer app for it was discovered. And that killer app is image processing.
Blog : The Incredible Convenience of Mathematica Image Processing
roots
John Baez December 15, 2011 Around 2006, my friend Dan Christensen created a fascinating picture of all the roots of all polynomials of degree ≤ 5 with integer coefficients ranging from -4 to 4: Click on the picture for bigger view.
PencilWise
PENCILWISE - Equation Analysis Test Take this "test" as your personal challenge. This test does not measure your intelligence, your fluency with words, and certainly not your mathematical ability.
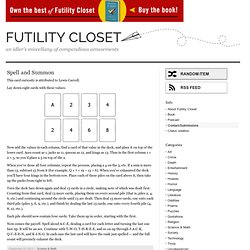
This card curiosity is attributed to Lewis Carroll. Lay down eight cards with these values: Now add the values in each column, find a card of that value in the deck, and place it on top of the lower card. Aces count as 1, jacks as 11, queens as 12, and kings as 13. Thus in the first column 1 + 2 = 3, so you’d place a 3 on top of the 2. When you’ve done all four columns, repeat the process, placing a 4 on the 3, etc.
Spell and Summon
Wonders of Math - The Game of Life
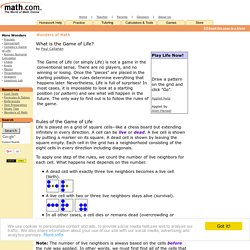
What is the Game of Life? by Paul Callahan Rules of the Game of Life Life is played on a grid of square cells--like a chess board but extending infinitely in every direction. A cell can be live or dead .The Socratic Method
This is a free sample with the opportunity at the end to download the full work for $0.50 (half dollar) by credit card or by PayPal account . The Socratic Method: Teaching by Asking Instead of by Telling by Rick Garlikov The following is a transcript of a teaching experiment, using the Socratic method, with a regular third grade class in a suburban elementary school. I present my perspective and views on the session, and on the Socratic method as a teaching tool, following the transcript. The class was conducted on a Friday afternoon beginning at 1:30, late in May, with about two weeks left in the school year.Scale/Ratio/Proportions
Your pearltree is like the best math collection I've ever seen;
The way those 45 pearls take over my screen is spooky
in a good way. In my spare time I'll be back to explore this. :) by virttree Oct 9