

Hilbert space - Поиск в Google. Hilbert Space Filling Curve Abstract Geometric Art. 15_03 11/2/2007 by Don Relyea I have been looking at the space filling curve project again recently.

The top 4 new images on this page were createdwith the latest version of the algorithm. 3D Model: 3D printed Hilbert curve. This model is a three-dimensional version of the space-filling Hilbert curve: The Hilbert curve is a recursive structure, so it is created by copying the same step of replacing line segments over and over again.
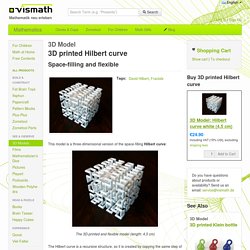
To get an idea of how this works take a look at the two-dimensional version: In every iteration a straight line segment is replaced by a curved one as shown in the left picture. New straigt segments emerge. In the next step, these segments get replaced. Alex's blog: A little bit about Hilbert space-filling curve. As a student I have investigated properties of different scanning algorithm to unwrap an N-dimensional array into one dimensional.
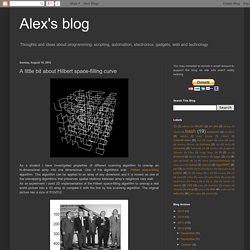
One of the algorithms was Hilbert space-filling algorithm. This algorithm can be applied to an array of any dimension and it is known as one of the unwrapping algorithms that preserves spatial relations between array's neighbors very well. Hilbert Space Filling Curve in 3D. Rob Eastaway - Home. PyTopMod2.223.zip - topmod - Python / Windows Version 2.223 (requires Python2.5) - Topological Mesh Modeler. Moebius Manifests. Hilbert curve 3d. Hilbert curve 3d. Efficient Calendars and space-filling curves. After demonstrating a useless method for implementing a square magnifier and writing this post, I think I’m going to start a category called Useless Mathematics.
So today, we talk about how to increase your productivity tenfold by revolutionising the traditional calendar layout. Take a calendar. The sequence of days isn’t continuous on the page: it’s broken when months change. You have to turn the page, or switch columns. So if some period of time in your overloaded planning spans across a month change, your calendar becomes messy. The idea isn’t new. Python: Hilbert Curve. Analogies from 2D to 3D Exercises in Disciplined Creativity. CarloH.

Séquin Abstract Human creativity reliesto a large part on our ability to recognize and match patterns, to transposethese patterns into different domains, and to find analogies in new domainsto known facts in old domains. In the realm of geometrical proofs and geometricalart, such analogies can carry concepts and methods from spaces that areeasy to deal with, e.g. drawings in a 2-dimensional plane, into higher dimensions where model making and visualization are much harder to carryout. Students in a graduate course on geometric modeling are challengedwith open-ended design exercises that introduce them to this analogicalreasoning and, hopefully, enhance their creative thinking abilities.
Fractales 3d. Sur les courbes de remplissage. L’idée que les courbes n’ont pas d’épaisseur et que par conséquent elles ont une aire nulle, qu’il y a moins de points dans un segment de droite qu’à l’intérieur d’un carré, était un héritage mathématique indiscuté depuis toujours ; mais finalement cette idée a dû être abandonnée.
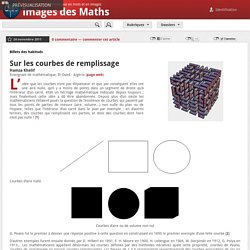
Depuis plus d’un siècle les mathématiciens s’étaient posés la question de l’existence de courbes qui passent par tous les points de parties de mesure (aire, volume...) non nulle du plan ou de l’espace, telles que l’intérieur d’un carré dans le plan par exemple ; en d’autres termes, des courbes qui remplissent ces parties, et donc des courbes dont l’aire n’est pas nulle ! Brevet EP1258054B1 - Antennes miniatures de remplissage de l'espace - Google Brevets. Fractales. Andrea Hawksley. I spent the last week in Tokyo, Japan attending the 6th meeting on Origami, Science, Math, and Education (6OSME). 6OSME is an amazing gathering of researchers from all of the many disciplines relating to origami (computer science, mathematics, engineering, architecture, etc.), as well as serious origami artists.
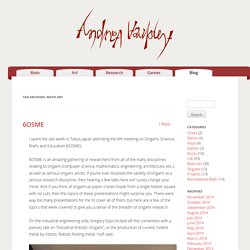
If you’ve ever doubted the validity of origami as a serious research discipline, then hearing a few talks here will surely change your mind. Recherche Flickr: origami spiral. Viereck Verlag - warenkorb. Модульное оригами как современное искусство. Современное искусство включает в себя такой стиль как оригами, которое имеет японские корни.
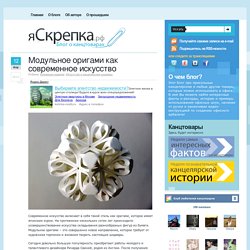
Origami Österreich. DesignLive on Shapeways. Two Points and More. Exploring more about three diameters I again wondered about one diameter and the first fold (continuation from last month) and what else I have not seen.
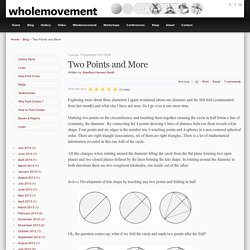
So I go over it one more time. Marking two points on the circumference and touching them together creasing the circle in half forms a line of symmetry, the diameter. By connecting the 4 points showing 6 lines of distance between them reveals a kite shape. Four points and six edges is the number ten; 6 touching points and 4 spheres in a non-centered spherical order. The Fitful Flog » Blog Archive » The Octuple Helix Compass Rose Jar. March 11, 2006 The Octuple Helix Compass Rose Jar Which is pretty much exactly the same as the previous model, the 8-Sided Compass Rose Jar.
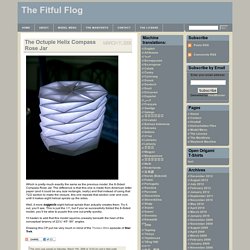
Spiral Triangles. Sacred Geometry. The Sacred mean - (5:8 or 1:1.618 or Φ) (The Divine Proportion, Golden Section, Golden ratio, Phi, ) One of the Key-stones of sacred geometry is the 'sacred mean' or 'golden section'. Vitruvian Man: Leonardo Da Vinci. One of the fundamental products of this underlying mathematical structure is the 'sacred mean', a mathematical constant which is visible across the spectrum of the natural world. Flick Dot Buzz . com - Cat Friendly Christmas Ornaments. =^..^= Flick =^..^= Dot =^..^= Buzz . com =^..^= Articles =^..^= Photos =^..^= Links =^..^= Stuff =^..^= Main =^..
The World's Best Photos of corrugation and origami. Flickr Hive Mind is a search engine as well as an experiment in the power of Folksonomies. All thumbnail images come directly from Flickr, none are stored on Flickr Hive Mind. These photos are bound by the copyright and license of their owners, the thumbnail links take to you to the photos (as well as their copyright and license details) within Flickr. Because some other search engines (Google, etc.) index parts of Flickr Hive Mind, you may have been led here from one of them. Welcome to Flickr Hive Mind, almost certainly the best search engine for photography on the web. How to Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines and a Circle. How to Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines and a Circle Using only a circle and straight lines, it's possible to create many different curves that are quite pleasing to look at and well known mathematically.
Most of the curves that are going to be explored in this post are featured at this site, which has a program for generating them, and this site which explores some of the geometry used in creating these curves. I recommend exploring both of them if you are going to create any of the designs below. I created all of these with a pencil and a ruler, or with the free computer program Geogebra. They could be created with any tool capable of making a straight line as discussed in the previous post on creating string art. Curve-stitch Isometric Cube. The figure above is an instance of a design I created more than forty years ago. (This figure is covered by a Creative Commons license. For more information, click here.) A framed version of it hangs on my kitchen wall. That picture is a negative print (i.e., white on black) of an India ink drawing on vellum.
It is a minor conversation piece—first-time viewers are often surprised to learn that the drawing contains no curves. The World's Best Photos of corrugation and origami. Spiral: Origami. Inkscape Tutorial: Drawing Origami Crease Patterns for Whirlpool Spirals. Download the vector graphics program Inkscape at: I was really pleased to see how excited people were about "Spiral: Origami | Art | Design" by Tomoko Fuse when I posted my video "review". That's why I decided to produce an additional video. It's a guide on how to draw the crease patterns for whirlpool spirals (and coil folds) with the method introduced in the book.
While the book explains the construction and gives angles etc., I figured not everyone would know good ways of simplifying the actual drawing process. Hence this video. So yes, it's probably a video that only makes sense if you have the book, but hopefully it will be a very helpful video for all those that do have or get it. And to those that don't have the book: You can download the example crease pattern I drew in the video.
P.S. Elephant Hide Review. Modular Origami Spiral (Tomoko Fuse)