

Modèles en jouet - Tadashi Tokieda. Crochet de Poisson. Un article de Wikipédia, l'encyclopédie libre.
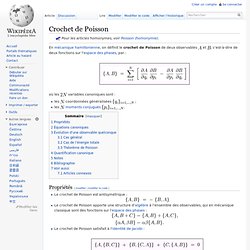
En mécanique hamiltonienne, on définit le crochet de Poisson de deux observables et , c'est-à-dire de deux fonctions sur l'espace des phases, par : où les. Automate cellulaire. Un article de Wikipédia, l'encyclopédie libre.
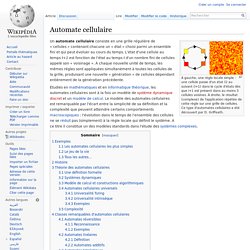
À gauche, une règle locale simple : une cellule passe d'un état (i) au suivant (i+1) dans le cycle d'états dès que i+1 est présent dans au moins 3 cellules voisines. À droite, le résultat (complexe) de l'application répétée de cette règle sur une grille de cellules. Ce type d'automates cellulaires a été découvert par D. Connectologie. Publications Espaces connectifs : représentations, feuilletages, ordres, difféologies, Cahiers de topologie et géométrie différentielle catégoriques LIV (2013) .

Fichier pdf. Dynamiques connectives (une introduction aux notions connectives : espaces, représentations, feuilletages et dynamiques catégoriques), Editions universitaires européennes, 2012. Cet ouvrage peut être commandé ici : Chaos theory. CHAOS: contrôle de systèmes chaotiques. Théorie du chaos. Un article de Wikipédia, l'encyclopédie libre.
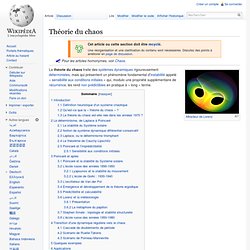
Pour les articles homonymes, voir Chaos. La théorie du chaos traite des systèmes dynamiques rigoureusement déterministes, mais qui présentent un phénomène fondamental d'instabilité appelé « sensibilité aux conditions initiales » qui, modulo une propriété supplémentaire de récurrence, les rend non prédictibles en pratique à « long » terme. Introduction[modifier | modifier le code] Définition heuristique d'un système chaotique[modifier | modifier le code] Un système dynamique est dit chaotique si une portion « significative » de son espace des phases présente simultanément les deux caractéristiques suivantes : La présence de ces deux propriétés entraîne un comportement extrêmement désordonné qualifié à juste titre de « chaotique ».
Qu'est-ce que la « théorie du chaos » ? La théorie du chaos. Théorie du chaos. Un article de Wikipédia, l'encyclopédie libre.
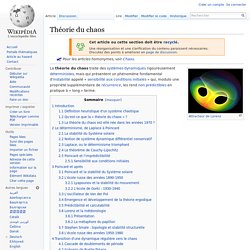
Pour les articles homonymes, voir Chaos. La théorie du chaos traite des systèmes dynamiques rigoureusement déterministes, mais qui présentent un phénomène fondamental d'instabilité appelé « sensibilité aux conditions initiales » qui, modulo une propriété supplémentaire de récurrence, les rend non prédictibles en pratique à « long » terme. Introduction[modifier | modifier le code] Séminaire " développement viable" juin 1996, Mèze. Chantal Kourilsky-Augeven Centre National de la Recherche Scientifique, France Index Liens La rubrique "Recherches" du RED&S contient un grand nombre de recherches faisant appel à des problématiques touchant à la viabilité, dans des disciplines variées : anthropologie, sociologie, droit.

Le site de l'Association de Modélisation de la Complexité (AE-MCX) comporte une grande bibliographie commentée (500 titres) et de nombreux travaux sur la pensée complexe et la gestion des ressources naturelles. 16-19 juin 1996 Programme. Décision Viabilité Systèmes dynamiques controlés. Géométrie hyperbolique. Un article de Wikipédia, l'encyclopédie libre.
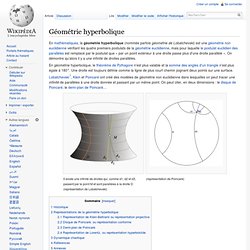
En mathématiques, la géométrie hyperbolique (nommée parfois géométrie de Lobatchevski) est une géométrie non euclidienne vérifiant les quatre premiers postulats de la géométrie euclidienne, mais pour laquelle le postulat euclidien des parallèles est remplacé par le postulat que « par un point extérieur à une droite passe plus d'une droite parallèle ». On démontre qu'alors il y a une infinité de droites parallèles. En géométrie hyperbolique, le théorème de Pythagore n'est plus valable et la somme des angles d'un triangle n'est plus égale à 180°.
Une droite est toujours définie comme la ligne de plus court chemin joignant deux points sur une surface. Ergodic theory. Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems.
Ergodic theory. Ergodic theory (Greek: έργον ergon "work", όδος hodos "way") is a branch of mathematics that studies dynamical systems with an invariant measure and related problems.
Its initial development was motivated by problems of statistical physics. The problem of metric classification of systems is another important part of the abstract ergodic theory. An outstanding role in ergodic theory and its applications to stochastic processes is played by the various notions of entropy for dynamical systems. Ergodic transformations[edit] Hypothèse ergodique. Un article de Wikipédia, l'encyclopédie libre.
L'hypothèse ergodique, ou hypothèse d'ergodicité, est une hypothèse fondamentale de la physique statistique. Elle fut formulée initialement par Ludwig Boltzmann en 1871 pour les besoins de sa théorie cinétique des gaz. Elle s'appliquait alors aux systèmes composés d'un très grand nombre de particules, et affirmait qu'à l'équilibre, la valeur moyenne d'une grandeur calculée de manière statistique est égale à la moyenne d'un très grand nombre de mesures prises dans le temps. La première valeur est celle que permet de calculer la physique statistique, la seconde est proche de ce qu'on peut expérimentalement mesurer.
Théorie ergodique. Un article de Wikipédia, l'encyclopédie libre. La théorie ergodique est une branche des mathématiques née de l'étude de l'hypothèse ergodique formulée par le physicien Ludwig Boltzmann en 1871 pour sa théorie cinétique des gaz. Elle a connu de nombreux développements en relation étroite avec la théorie des systèmes dynamiques et la théorie du chaos.
Notations[modifier | modifier le code] Dynamique discrète[modifier | modifier le code] L'objet d'étude en théorie ergodique est un triplet où : Théorie Ergodique- Elon Lindenstrauss. Elon Lindenstrauss vient de recevoir la médaille Fields « Pour ses résultats sur la rigidité des mesures en théorie ergodique, et leurs applications à la théorie des nombres. » Elon Lindenstrauss a développé des outils théoriques extraordinairement puissants en théorie ergodique, un champ des mathématiques originellement conçu pour comprendre la mécanique céleste. Sa très bonne compréhension de la théorie ergodique lui a ensuite permis de les utiliser pour résoudre une série de problèmes importants dans des domaines mathématiques apparemment très éloignés. Langage MGS Modeling dynamical system with a dynamical structure. Computational Models for Integrative and Developmental Biology. Magnus effect. Mixing (mathematics) Mixing in a ball of colored putty after consecutive iterations of "Smale horseshoe map" (i.e. squashing and folding in two) Let be a sequence of random variables.
Such a sequence is naturally endowed with a topology, the product topology. Du mouvement des systèmes dynamiques. Théorème de Cauchy-Lipschitz. Un article de Wikipédia, l'encyclopédie libre. Certaines lois physiques, comme le principe fondamental de la dynamique, se traduisent par des équations différentielles vérifiant les hypothèses du théorème. Ce dernier assure alors le caractère déterministe du mécanisme décrit par la loi. Uncertainty. We are frequently presented with situations wherein a decision must be made when we are uncertain of exactly how to proceed. Uncertainty is a term used in subtly different ways in a number of fields, including philosophy, physics, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially observable and/or stochastic environments, as well as due to ignorance and/or indolence.[1]
Uncertainty quantification. Uncertainty quantification (UQ) is the science of quantitative characterization and reduction of uncertainties in applications.