

Hausdorff dimension. In mathematics, the Hausdorff dimension (also known as the Hausdorff–Besicovitch dimension) is an extended non-negative real number associated with any metric space.
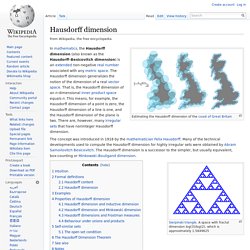
Sierpinski triangle. Sierpinski triangle Generated using a random algorithm The Sierpinski triangle (also with the original orthography Sierpiński), also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles.
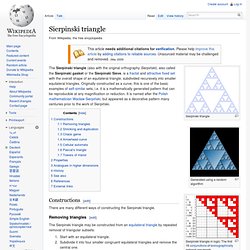
Originally constructed as a curve, this is one of the basic examples of self-similar sets, i.e. it is a mathematically generated pattern that can be reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries prior to the work of Sierpiński. Constructions[edit] There are many different ways of constructing the Sierpinski triangle. Removing triangles[edit] The Sierpinski triangle may be constructed from an equilateral triangle by repeated removal of triangular subsets: Shrinking and duplication[edit] Chaos game[edit] , and Or more simply: Arrowhead curve[edit] . Emergence. Snowflakes forming complex symmetrical patterns is an example of emergence in a physical system.
In philosophy, systems theory, science, and art, emergence is the way complex systems and patterns arise out of a multiplicity of relatively simple interactions. Emergence is central to the theories of integrative levels and of complex systems. Biology can be viewed as an emergent property of the laws of chemistry which, in turn, can be viewed as an emergent property of particle physics. Similarly, psychology could be understood as an emergent property of neurobiological dynamics, and free-market theories understand economy as an emergent feature of psychology. Boundary value problem. Cantor set. In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties.
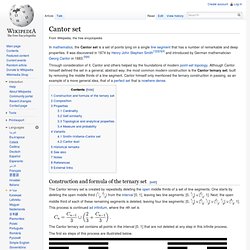
It was discovered in 1874 by Henry John Stephen Smith[1][2][3][4] and introduced by German mathematician Georg Cantor in 1883.[5][6] Through consideration of it, Cantor and others helped lay the foundations of modern point-set topology. Although Cantor himself defined the set in a general, abstract way, the most common modern construction is the Cantor ternary set, built by removing the middle thirds of a line segment.
Cantor himself only mentioned the ternary construction in passing, as an example of a more general idea, that of a perfect set that is nowhere dense. Construction and formula of the ternary set[edit] The Cantor ternary set contains all points in the interval [0, 1] that are not deleted at any step in this infinite process. The first six steps of this process are illustrated below. Attractor. Visual representation of a strange attractor In dynamical systems, an attractor is a set of physical properties toward which a system tends to evolve, regardless of the starting conditions of the system.[1] Property values that get close enough to the attractor values remain close even if slightly disturbed.
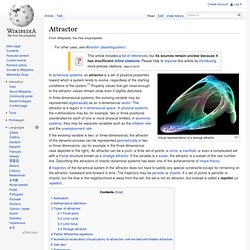
A trajectory of the dynamical system in the attractor does not have to satisfy any special constraints except for remaining on the attractor, backward and forward in time. The trajectory may be periodic or chaotic. If a set of points is periodic or chaotic, but the flow in the neighborhood is away from the set, the set is not an attractor, but instead is called a repeller (or repellor). Motivation[edit] A dynamical system is generally described by one or more differential or difference equations. Dynamical systems in the physical world tend to arise from dissipative systems: if it were not for some driving force, the motion would cease.
Mathematical definition[edit] Sierpinski carpet. The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916.
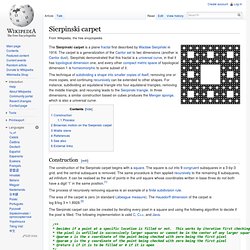
The carpet is a generalization of the Cantor set to two dimensions (another is Cantor dust). Sierpiński demonstrated that this fractal is a universal curve, in that it has topological dimension one, and every other compact metric space of topological dimension 1 is homeomorphic to some subset of it. The technique of subdividing a shape into smaller copies of itself, removing one or more copies, and continuing recursively can be extended to other shapes. For instance, subdividing an equilateral triangle into four equilateral triangles, removing the middle triangle, and recursing leads to the Sierpinski triangle. In three dimensions, a similar construction based on cubes produces the Menger sponge, which is also a universal curve.
Fractal. Figure 1a.
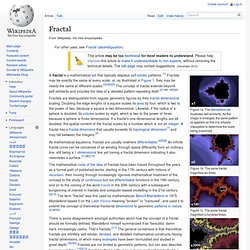
The Mandelbrot set illustrates self-similarity. As the image is enlarged, the same pattern re-appears so that it is virtually impossible to determine the scale being examined. Figure 1b. The same fractal magnified six times. Figure 1c. Figure 1d. Fractals are distinguished from regular geometric figures by their fractal dimensional scaling. As mathematical equations, fractals are usually nowhere differentiable.[2][5][8] An infinite fractal curve can be conceived of as winding through space differently from an ordinary line, still being a 1-dimensional line yet having a fractal dimension indicating it also resembles a surface.[7]:48[2]:15 There is some disagreement amongst authorities about how the concept of a fractal should be formally defined. Introduction[edit] The word "fractal" often has different connotations for laypeople than mathematicians, where the layperson is more likely to be familiar with fractal art than a mathematical conception.
History[edit] Figure 2.