

Scott Draves - Software Artist. Scott Draves. First of all I want to thank two incredible people who made possible this amazing Special Post, the well known software artist Scott Draves and as interviewer Phoenix Perry who is curator of Devotion Gallery and a new media artist and performer.

So in the interview you can read almost everything about the career of Scott Draves as a visual and software artist. He says how and when started in the fabulous and huge world of programming and also explains some of his projects in the easy way. If you already know him, now you're going to learn a lot of new stuff from him, and if you didn't hear speaking about him, so you'll meet a pioneer of generative art and the creator of the Electric Sheep.
See more; Scott Draves (S) and Phoenix Perry (P) P: Hi! S: Hi Phoenix. P: Have you always been hooked on art through programming? S: I started programming in about 1978 when I was 10 years old. Apophysis.org. Www.chaoticafractals.com. Audio slideshow: The art of mathematics. To the untrained eye, these vivid images might appear to be random sets of colourful swirls and circles.
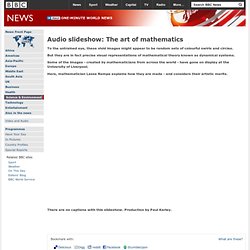
But they are in fact precise visual representations of mathematical theory known as dynamical systems. Some of the images - created by mathematicians from across the world - have gone on display at the University of Liverpool. Here, mathematician Lasse Rempe explains how they are made - and considers their artistic merits. <table cellspacing="0" cellpadding="0" border="0" width="352" align="center"><tr><td><table cellspacing="1" cellpadding="30" border="0" bgcolor="#cccccc" width="100%" height="33"><tr><td bgcolor="#fafafa"><div class="font-family:Verdana;color:#666666;font-size:11px;"><span style="font-family:Verdana;color:#333333;font-size:18px;font-weight:800;"><strong>Javascript and Flash plug-in required</strong></span><P>Either the Flash plugin was not detected on your computer or the JavaScript features of your brower have been disabled.
Fractal flame. Fractal flames differ from ordinary iterated function systems in three ways: Nonlinear functions are iterated instead of affine transforms.Log-density display instead of linear or binary (a form of tone mapping)Color by structure (i.e. by the recursive path taken) instead of monochrome or by density.
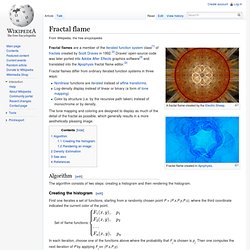
The tone mapping and coloring are designed to display as much of the detail of the fractal as possible, which generally results in a more aesthetically pleasing image. Algorithm[edit] The algorithm consists of two steps: creating a histogram and then rendering the histogram. Creating the histogram[edit] First one iterates a set of functions, starting from a randomly chosen point P = (P.x,P.y,P.c), where the third coordinate indicated the current color of the point. Set of flame functions: In each iteration, choose one of the functions above where the probability that Fj is chosen is pj. Koch snowflake.
The first seven iterations in animation Zooming into the Koch curve The Koch snowflake (also known as the Koch star and Koch island[1]) is a mathematical curve and one of the earliest fractal curves to have been described.
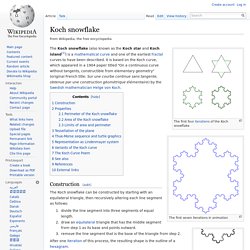
It is based on the Koch curve, which appeared in a 1904 paper titled "On a continuous curve without tangents, constructible from elementary geometry" (original French title: Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire) by the Swedish mathematician Helge von Koch. Construction[edit] The Koch snowflake can be constructed by starting with an equilateral triangle, then recursively altering each line segment as follows: divide the line segment into three segments of equal length.draw an equilateral triangle that has the middle segment from step 1 as its base and points outward.remove the line segment that is the base of the triangle from step 2. List of fractals by Hausdorff dimension. Deterministic fractals[edit] Random and natural fractals[edit] See also[edit]
Fractal art. Fractal art is a form of algorithmic art created by calculating fractal objects and representing the calculation results as still images, animations, and media.
Fractal art developed from the mid-1980s onwards.[1] It is a genre of computer art and digital art which are part of new media art. The Julia set and Mandelbrot sets can be considered as icons of fractal art.[2] Fractal art (especially in the western world) is not drawn or painted by hand. It is usually created indirectly with the assistance of fractal-generating software, iterating through three phases: setting parameters of appropriate fractal software; executing the possibly lengthy calculation; and evaluating the product. In some cases, other graphics programs are used to further modify the images produced.
Types[edit] A 3D Mandelbulb fractal generated using Visions of Chaos There are many different kinds of fractal images and can be subdivided into several groups. L-system. L-system trees form realistic models of natural patterns Origins[edit] 'Weeds', generated using an L-system in 3D. As a biologist, Lindenmayer worked with yeast and filamentous fungi and studied the growth patterns of various types of algae, such as the blue/green bacteria Anabaena catenula. Originally the L-systems were devised to provide a formal description of the development of such simple multicellular organisms, and to illustrate the neighbourhood relationships between plant cells. Later on, this system was extended to describe higher plants and complex branching structures.