

Discontinuous derivative. Non-analytic smooth function. The existence of smooth but non-analytic functions represents one of the main differences between differential geometry and analytic geometry.
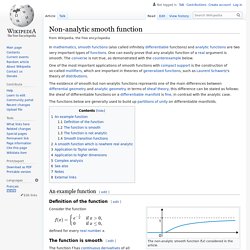
In terms of sheaf theory, this difference can be stated as follows: the sheaf of differentiable functions on a differentiable manifold is fine, in contrast with the analytic case. The functions below are generally used to build up partitions of unity on differentiable manifolds. Definition of the function[edit] The non-analytic smooth function considered in the article. Consider the function defined for every real number x.
The function is smooth[edit] The function f has continuous derivatives of all orders in all points x of the real line, given by where pn(x) is a polynomial of degree n − 1 given recursively by p1(x) = 1 and Outline of proof[edit] The proof, by induction, is based on the fact that for any natural number m including zero, which implies that all f (n) are continuous and differentiable at x = 0, because Detailed proof[edit] Calculus III. Show Mobile NoticeShow All NotesHide All Notes You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone).

Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width. Here are my online notes for my Calculus III course that I teach here at Lamar University. Despite the fact that these are my “class notes”, they should be accessible to anyone wanting to learn Calculus III or needing a refresher in some of the topics from the class. These notes do assume that the reader has a good working knowledge of Calculus I topics including limits, derivatives and integration.
Here are a couple of warnings to my students who may be here to get a copy of what happened on a day that you missed. Fractional Calculus III. The discussion about fractional calculus, which led to this series of articles, was started by a couple of sixth form students on the askNRICH webboard.
Before reading this article you may like to read the first two articles Fractional Calculus I and Fractional Calculus II and see the conversation on the webboard. Derivatives and integrals Given a function f(x) we can differentiate it once, twice, and so on in the usual way. We can also integrate the function once, twice, and so on to get (If)(x), (I^2f)(x),\ldots, and now we can even get (I^af)(x) for any positive a. We are used to the idea that differentiation 'reverses' the process of integration, and this is just the formula \frac{d}{dx}(If)(x) = \frac{d}{dx}\int_0^x f(t)\,dt = f(x). Note however, that integrating from 0 to x (that is, calculating (If)(x)) does NOT reverse differentiation. Derivatives of integrals Suppose that p and q are integers, and that p> q.
And repeating this process q-1 more times gives the result. Fractional Calculus I. Introduction There has been a lot of correspondence recently on the Ask Nrich web-board about fractional derivatives.
We know how to differentiate a function once, twice and so on, but can we differentiate the function 3/2 times? Similarly, we know how to integrate a function once, twice, and so on, but can we integrate it 1/2 times? This is the first of three articles which will introduce you to the main ideas in this new and rather strange world of fractional integrals and derivatives. Questions about the existence of such things were asked not long after calculus was created; for example, in 1695 Leibnitz wrote "Thus it follows that will be equal to from which one day useful consequences will be drawn . " PDE Web Application. Chapter11.pdf.
Big o - What is the difference between Θ(n) and O(n)? Dr. Dougherty's Differential Equations I Assignment Page. Faculty.swosu.edu - /michael.dougherty/book/