

Calculus - Reversing the Order of Integration and Summation. Real analysis - When can a sum and integral be interchanged? Can infinite sums and integrals be swapped anytime? Measure theory - Is there an example of a sigma algebra that is not a topology? - Mathematics Stack Exchange. The Inscribed Squares Problem. These pages give a brief and informal introduction to one of my favorite unsolved mathematics problems -- the so-called "inscribed squares problem".

The question can be informally stated as follows: Notice that we don't care whether or not the square "stays inside" of the curve -- in fact, its sides may cross the curve many times. Nor do we care whether or not the corners of the square appear on the curve in any particular order. A more exact statement of the question requires a couple of (fairly simple) definitions. A simple closed curve is the image in the plane R2 of a continuous function f: [0,1] ----> R2 that is one-to-one except that f(0) = f(1). Possibility Two: "Most" simple closed curves do not have inscribed squares. Given that we can't rule out either of these extremes, how much is known? The first theorem shows that the "nice" behavior demanded by Stromquist's Theorem can be replaced by symmetry -- a different type of "nice" behavior.
Exercises Open Questions Visit my homepage.
10 Things to Know About Causal Inference. Macartan Humphreys (Ph.D., Harvard, 2003) works on the political economy of development and formal political theory.

Ongoing research focuses on civil wars, post-conflict development, ethnic politics, natural resource management, political authority and leadership, and democratic development with a current focus on the use of field experiments to study democratic decision-making in post-conflict and developing areas. He has conducted field research in Chad, Ghana, Haiti, Indonesia, Liberia, Mali, Sao Tome and Principe, Sierra Leone, Senegal, Uganda, and elsewhere. Recent work has appeared in the American Political Science Review, World Politics, the Economic Journal, and elsewhere. He has authored or coauthored books on ethnic politics, natural resource management, and game theory and politics. Matrix decomposition.
Representation of a matrix as a product Example[edit] In numerical analysis, different decompositions are used to implement efficient matrix algorithms.
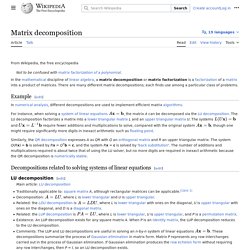
For instance, when solving a system of linear equations , the matrix A can be decomposed via the LU decomposition. Matrici Aggiunte e Matrici Trasposte. Real analysis - How come rearrangement of a convergent series may not converge to the same value / or does not converge at all. Raising a Number to a Complex Power. Number theory - Proving Irrationality. Theory behind the t-test. Assumptions for the t-test. What assumptions are made when conducting a t-test?
Reinforcement Learning. Propositional calculus - Wikipedia. Propositional calculus (also called propositional logic, sentential calculus, sentential logic, or sometimes zeroth-order logic) is the branch of logic concerned with the study of propositions (whether they are true or false) that are formed by other propositions with the use of logical connectives, and how their value depends on the truth value of their components.
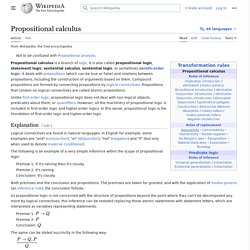
Logical connectives are found in natural languages. In English for example, some examples are "and" (conjunction), "or" (disjunction), "not” (negation) and "if" (but only when used to denote material conditional). The following is an example of a very simple inference within the scope of propositional logic: Premise 1: If it's raining then it's cloudy. Premise 2: It's raining. Conclusion: It's cloudy. Both premises and the conclusion are propositions. Premise 1: Premise 2: Conclusion: The same can be stated succinctly in the following way: History[edit] Propositional logic was eventually refined using symbolic logic. Argument[edit] . Semigroup. The binary operation of a semigroup is most often denoted multiplicatively: x·y, or simply xy, denotes the result of applying the semigroup operation to the ordered pair (x, y).
Associativity is formally expressed as that (x·y)·z = x·(y·z) for all x, y and z in the semigroup. Definition[edit] Superellipse. Examples of superellipses for A superellipse, also known as a Lamé curve after Gabriel Lamé, is a closed curve resembling the ellipse, retaining the geometric features of semi-major axis and semi-minor axis, and symmetry about them, but a different overall shape.
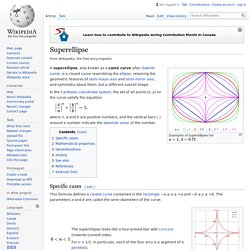
In the Cartesian coordinate system, the set of all points (x, y) on the curve satisfy the equation where n, a and b are positive numbers, and the vertical bars | | around a number indicate the absolute value of the number. Superformula. Some superformula samples: a=b=1; m, n1, n2 and n3 are shown in picture.
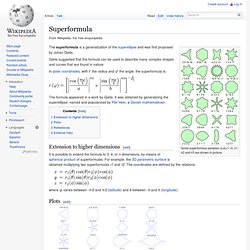
The superformula is a generalization of the superellipse and was first proposed by Johan Gielis. Gielis suggested that the formula can be used to describe many complex shapes and curves that are found in nature. In polar coordinates, with. Floor and ceiling functions - Wikipedia. Mathematical functions rounding a number to the two closest integers Floor function Ceiling function The integral part or integer part of x, often denoted [x] is usually defined as the ⌊x⌋ if x is nonnegative, and ⌈x⌉ otherwise. Useful Properties of the Floor and Ceil Functions. This articles explores some basic properties of the integer functions commonly known as floor and ceil.

Most of the statements may seem trivial or obvious, but I, for one, have a tendency to forget just how exact you can be when it comes to expressions/equations where floor or ceil functions appear. First, the definitions: ⌊x⌋=max{n∈Z∣n≤x} = the greatest integer less than or equal to x,⌈x⌉=min{n∈Z∣n≥x} = the least integer greater than or equal to x, for every real number x. Equality.
Understanding 4D. Taxonomy of Complex Matrices - List of matrices - Wikipedia. Several important classes of matrices are subsets of each other.
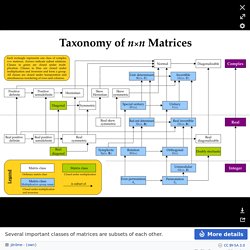
Further ways of classifying matrices are according to their eigenvalues or by imposing conditions on the product of the matrix with other matrices. Finally, many domains, both in mathematics and other sciences including physics and chemistry have particular matrices that are applied chiefly in these areas. Matrices with explicitly constrained entries[edit] The following lists matrices whose entries are subject to certain conditions.
List of matrices - Wikipedia. Several important classes of matrices are subsets of each other.
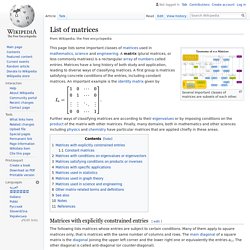
Further ways of classifying matrices are according to their eigenvalues or by imposing conditions on the product of the matrix with other matrices. Finally, many domains, both in mathematics and other sciences including physics and chemistry have particular matrices that are applied chiefly in these areas. Matrices with explicitly constrained entries[edit] The following lists matrices whose entries are subject to certain conditions. Mathematics Lectures. Diagram topological vector space. Copula (probability theory) Sklar's Theorem states that any multivariate joint distribution can be written in terms of univariate marginal distribution functions and a copula which describes the dependence structure between the variables. Copulas are popular in high-dimensional statistical applications as they allow one to easily model and estimate the distribution of random vectors by estimating marginals and copulae separately.
There are many parametric copula families available, which usually have parameters that control the strength of dependence. Some popular parametric copula models are outlined below. Corso di Borsa e Trading On Line. Con la nascita della borsa si sono ricercate, sviluppate e consolidate una serie di teorie specifiche dei mercati finanziari, sia di tipo scientifico/statistico sia di tipo non convenzionale come le teorie di Down, Elliott e Gann.
List of mathematical identities. Ineq. (uni)quation.
Statistical Learning Theory. Infinitesimal generator. Ornstein-Uhlenbeck processes. Hilbert spaces. Bounds. Probability. Encyclopedia of Mathematics. Calculus. Diagram of special function relationships. Abstract Modern Algebra. High Dimensional Statistics. Big Data. Geometry and Optimization. Topology. Recreational Math. Mathematics Resources.