

(26) The ANTI OLOID is one weird shape. Gömböc—The Shape That Shouldn't Exist. These Are the Biggest Numbers in Mathematics. Counting to three is so easy, a salamander can do it.

Seriously. Lab experiments have shown that captive salamanders are able to distinguish between piles of two fruit flies and piles of three. If you're not impressed, we understand. A human being who'd never taken a single math class would have no trouble doing the same thing. Some single-digit numbers like one, two and three are so small that our minds can recognize their value without even needing to count. Yet as numbers grow bigger, our ability to comprehend their values starts to break down. HOW QUICKLY CAN YOU CRACK THE CODE? What Mathematics Reveals About the Secret of Lasting Relationships and the Myth of Compromise.
In his sublime definition of love, playwright Tom Stoppard painted the grand achievement of our emotional lives as “knowledge of each other, not of the flesh but through the flesh, knowledge of self, the real him, the real her, in extremis, the mask slipped from the face.”

But only in fairy tales and Hollywood movies does the mask slip off to reveal a perfect other. Did artists lead the way in mathematics? Mathematics and art are generally viewed as very different disciplines – one devoted to abstract thought, the other to feeling.
But sometimes the parallels between the two are uncanny. From Islamic tiling to the chaotic patterns of Jackson Pollock, we can see remarkable similarities between art and the mathematical research that follows it. The two modes of thinking are not exactly the same, but, in interesting ways, often one seems to foreshadow the other. Does art sometimes spur mathematical discovery? There’s no simple answer to this question, but in some instances it seems very likely. Pi and the Great Pyramid. It was John Taylor who first proposed the idea that the number &pi might have been intentionally incorporated into the design of the Great Pyramid of Khufu at Giza.

He discovered that if one divides the perimeter of the Pyramid by its height, one obtains a close approximation to 2&pi. He compared this to the fact that if one divides the circumference of a circle by its radius, one obtains 2&pi. He suggested that perhaps the Great Pyramid was intended to be a representation of the spherical Earth, the height corresponding to the radius joining the center of the Earth to the North Pole and the perimeter corresponding to the Earth's circumference at the Equator. Taylor's ideas were presented in his book The Great Pyramid: Why Was It Built?
How to cheat at dice – from an expert in games. Archaeologists recently uncovered a 600-year-old die that was probably used for cheating.
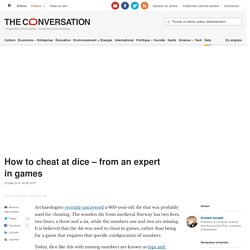
The wooden die from medieval Norway has two fives, two fours, a three and a six, while the numbers one and two are missing. It is believed that the die was used to cheat in games, rather than being for a game that requires that specific configuration of numbers. Today, dice like this with missing numbers are known as tops and bottoms. They can be a useful way to cheat if you’re that way inclined, although they don’t guarantee a win every time and they don’t stand up to scrutiny from suspicious opponents (they only have to ask to take a look and you’ll be found out).
But there are several other options of cheating at dice too, and I’ll talk you through some of them here. It should be noted that using these methods in a casino are illegal and I’m not suggesting you adopt them in such establishments – but it’s an interesting look at how probabilities work. Make a Sugihara Circle/Square Optical Illusion Out of Paper – David Richeson: Division by Zero. Yesterday I explained the mathematics behind Sugihara’s Circle/Square Optical Illusion, which appears in this video.
Today I created a printable template from which you can make your own version of Sugihara’s object. Click the following image to download the pdf. Data science can help us fight human trafficking. July 30 marks the United Nations’ World Day Against Trafficking in Persons, a day focused on ending the criminal exploitation of children, women and men for forced labor or sex work.
Between 27 and 45.8 million individuals worldwide are trapped in some form of modern-day slavery. The victims are forced into slavery as sex workers, beggars and child soldiers, or as domestic workers, factory workers and laborers in manufacturing, construction, mining, commercial fishing and other industries. Human trafficking occurs in every country in the world, including the U.S. It’s a hugely profitable industry, generating an estimated US$150 billion annually in illegal profits per year. Why crowds aren’t always wise: Lessons from mini-flash crashes on Wall Street.
Blink.
About 300 milliseconds just passed, the same time required for a lightning bolt to travel 100,000 feet, a satellite to fly two miles or a stock price to swing from US$10 to $0.0001 and back. Wait, what? Indeed, that actually happened to the shares of the software company Qualys a few years ago. What are the most widely practiced religions of the world? Facebook users worldwide 2017.
Binary to Decimal Converter. In order to use this new binary to decimal converter tool, type any binary value like 1010 into the left field below, and then hit the Convert button.
You can see the result in the right field below. It is possible to convert up to 63 binary characters to decimal. Binary to decimal conversion result in base numbers Binary System. We Feel Fine / mission. Mission We Feel Fine is an exploration of human emotion on a global scale.

Since August 2005, We Feel Fine has been harvesting human feelings from a large number of weblogs. Every few minutes, the system searches the world's newly posted blog entries for occurrences of the phrases "I feel" and "I am feeling". When it finds such a phrase, it records the full sentence, up to the period, and identifies the "feeling" expressed in that sentence (e.g. sad, happy, depressed, etc.).
Because blogs are structured in largely standard ways, the age, gender, and geographical location of the author can often be extracted and saved along with the sentence, as can the local weather conditions at the time the sentence was written. The result is a database of several million human feelings, increasing by 15,000 - 20,000 new feelings per day. Why 13532385396179 Is a Magic Number. Way up in the trillions, lost among so many very big numbers, lurks a hidden gem. It's 13532385396179, or written out: thirteen trillion, five hundred and thirty-two billion, three hundred and eighty-five million, three hundred and ninety-six thousand, one hundred seventy-nine.
Bakhshali Manuscript, Ancient Indian Mathematics - Ancient Science. The Bakhshali Manuscript is an Ancient Indian mathematical manuscript written on birch bark which was found near the village of Bakhshali in 1881 in what was then the North-West Frontier Province of British India (now Khyber Pakhtunkhwa province, in Pakistan). It’s written in Śāradā script and in Gatha dialect (which is a combination of the ancient Indian languages of Sanskrit and Prakrit). The manuscript is incomplete, with only seventy leaves of birch bark, many of which are mere scraps. Many remain undiscovered.
Blaise Pascal. Blaise Pascal was a French mathematician, physicist and religious philosopher, who laid the foundation for the modern theory of probabilities. Synopsis Mathematician Blaise Pascal was born on June 19, 1623, in Clermont-Ferrand, France. The Mathematics of Winning Monopoly. Hannah Fry: The mathematics of love. From 1,000,000 to Graham's Number. Welcome to numbers post #2. Last week, we started at 1 and slowly and steadily worked our way up to 1,000,000. We used dots. It was cute. Islamic Mathematics. The Islamic Empire established across Persia, the Middle East, Central Asia, North Africa, Iberia and parts of India from the 8th Century onwards made significant contributions towards mathematics.
Are there right angles in nature? Hertha Marks Ayrton. The World Population and me - Population games. The Alan Turing Year - <b>TCAC ACC</b> Conway's Game of Life - Javascript/Canvas Implementation. BBC Four - The Secret Rules of Modern Living: Algorithms. Revolutions: data science. By Sherri RoseAssistant Professor of Health Care PolicyHarvard Medical School Targeted learning methods build machine-learning-based estimators of parameters defined as features of the probability distribution of the data, while also providing influence-curve or bootstrap-based confidence internals. The theory offers a general template for creating targeted maximum likelihood estimators for a data structure, nonparametric or semiparametric statistical model, and parameter mapping.
Worldometers - real time world statistics. Bach and the mathematics of genius. Learn morse code. Hannah Fry. Dr Hannah Fry: the mathematical models that underpin our sexual success. BBC Four - Climate Change by Numbers. Monte Carlo method. Monte Carlo methods (or Monte Carlo experiments) are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results; typically one runs simulations many times over in order to obtain the distribution of an unknown probabilistic entity. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to obtain a closed-form expression, or infeasible to apply a deterministic algorithm.
Monte Carlo methods are mainly used in three distinct problem classes: optimization, numerical integration and generation of draws from a probability distribution. The modern version of the Monte Carlo method was invented in the late 1940s by Stanislaw Ulam, while he was working on nuclear weapons projects at the Los Alamos National Laboratory. Immediately after Ulam's breakthrough, John von Neumann understood its importance and programmed the ENIAC computer to carry out Monte Carlo calculations. Introduction[edit] Ding Dong Bell. Divide By Zero. About To Divide by Zero is an internet slang term describing an action that leads to an epic failure or theoretically unlikely disaster, such as an earth-shattering apocalypse or a wormhole in the time-space continuum. Podcasts and Downloads - More or Less: Behind the Stats. Library.thinkquest.org/3703/
As of July 1, 2013 ThinkQuest has been discontinued. We would like to thank everyone for being a part of the ThinkQuest global community: Golden ratio. The Fibonacci Numbers and Golden section in Nature - 1. Chaos & Fractals. Chaos Theory and Complexity Theory: A non-technical introduction to the science of Chaos and Complexity. Double Pendulum. Chaotic Pendulum. Chaotic Pendulum.