

Review : Trig Functions. The intent of this section is to remind you of some of the more important (from a Calculus standpoint…) topics from a trig class.
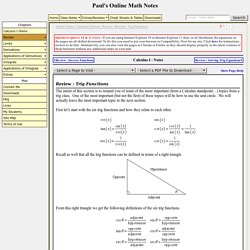
One of the most important (but not the first) of these topics will be how to use the unit circle. We will actually leave the most important topic to the next section. Review : Solving Trig Equations. Example 3 Solve on Solution This problem is very similar to the other problems in this section with a very important difference.
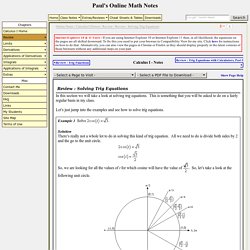
We’ll start this problem in exactly the same way. We first need to find all possible solutions. So, we are looking for angles that will give out of the sine function. Now, there are no angles in the first quadrant for which sine has a value of. . . , so the angle in the third quadrant will be below the negative x-axis or . Below the positive x-axis or . Now we come to the very important difference between this problem and the previous problems in this section. This is not the set of solutions because we are NOT looking for values of x for which , but instead we are looking for values of x for which . . Well, actually, that’s not quite the solution. Notice that we also divided the by 5 as well! I’ll leave it to you to verify my work showing they are solutions.
By 5 you would have missed these solutions! N = 0. n = 1. n = 2. n = 3. n = 4. n = 5. n = 1 . Radians to degrees. How to convert degrees to radians or radians to degrees.

Theory: What are 'radians' ? One radian is the angle of an arc created by wrapping the radius of a circle around its circumference. Graphs of Sine, Cosine and Tangent. Here are some nice graphs to look at ...

Plot of Sine The Sine Function has this beautiful up-down curve (which repeats every 2π radians, or 360°). It starts at 0, heads up to 1 by π/2 radians (90°) and then heads down to -1. Plot of Cosine Cosine is just like Sine, but it starts at 1 and heads down until π radians (180°) and then heads up again. Plot of Sine and Cosine In fact Sine and Cosine are like good friends: they follow each other, exactly "π/2" radians, or 90°, apart. Plot of the Tangent Function The Tangent function has a completely different shape ... it goes between negative and positive Infinity, crossing through 0 (every π radians, or 180°), as shown on this plot. At π/2 radians, or 90° (and -π/2, 3π/2, etc) the function is officially undefined, because it could be positive Infinity or negative Infinity. Inverse Sine, Cosine and Tangent The Inverse Sine, Cosine and Tangent graphs are: Inverse Sine Inverse Cosine Inverse Tangent Mirror Images.
Graphing Trigonometric Functions. Graphing Trigonometric Functions (page 1 of 3) Sections: Introduction, Examples with amplitude and vertical shift, Example with phase shift You've already learned the basic trig graphs.
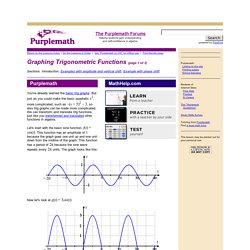
But just as you could make the basic quadratic x2, more complicated, such as –(x + 5)2 – 3, so also trig graphs can be made more complicated. We can transform and translate trig functions, just like you transformed and translated other functions in algebra. Let's start with the basic sine function, f(t) = sin(t). Now let's look at g(t) = 3sin(t): Do you see that the graph is three times as tall? Now let's look at h(t) = sin(2t): Copyright © Elizabeth Stapel 2010 All Rights Reserved. Interactive Unit Circle. Amplitude, Period, Phase Shift and Frequency.
Some functions (like Sine and Cosine) repeat forever and are called Periodic Functions.
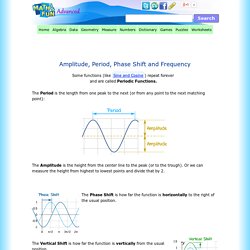
The Period is the length from one peak to the next (or from any point to the next matching point): The Amplitude is the height from the center line to the peak (or to the trough). Or we can measure the height from highest to lowest points and divide that by 2. The Phase Shift is how far the function is horizontally to the right of the usual position.
The Vertical Shift is how far the function is vertically from the usual position. All Together Now! We can have all of them in one equation: y = A sin(Bx + C) + D amplitude is A period is 2π/B phase shift is −C/B vertical shift is D. MA301 Trigonometric Functions.