Trigonometry
Trigonometry (from Greek trigonon "triangle" + metron "measure") Want to learn Trigonometry? Here is a quick summary.
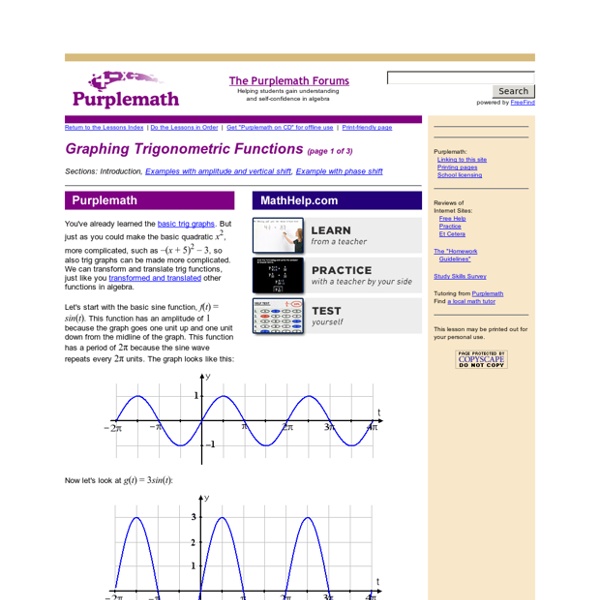
Basic Trigonometric Graphs
Trigonometric Functions and Their Graphs: The Sine and Cosine (page 1 of 3) Sections: The sine and cosine, The tangent, The co-functions At first, trig ratios related only to right triangles. Then you learned how to find ratios for any angle, using all four quadrants. Then you learned about the unit circle, in which the value of the hypotenuse was always r = 1 so that sin(θ) = y and cos(θ) = x. In other words, you progressed from geometrical figures to a situation in which there was just one input (one angle measure, instead of three sides and an angle) leading to one output (the value of the trig ratio).
Lesson HOW TO - Solve Trigonometric equations
Introduction The solution of trigonometric equations is one topic that students have particular problems with. There are a few reasons for this: 1. there is usually a simplify part first that requires use of some TRIG identities. 2. there is the use of RADIANS rather than degrees, for which some students are not at ease with. 3. there is the repetitive aspect of TRIG functions that students find bewildering. All in all, a potentially daunting topic. To be honest though, there is nothing that you need fear here, so long as you take it methodically and slowly.
SOLVING TRIGONOMETRIC EQUATIONS
Note: If you would like a review of trigonometry, click on trigonometry. Example 1: Solve for x in the following equation. There are an infinite number of solutions to this problem. First isolate the cosine term. To solve for x, we have to isolate x. How do we isolate the x?
Amplitude, Period, Phase Shift and Frequency
Some functions (like Sine and Cosine) repeat forever and are called Periodic Functions. The Period is the length from one peak to the next (or from any point to the next matching point): The Amplitude is the height from the center line to the peak (or to the trough).
Unit Circle
The "Unit Circle" is a circle with a radius of 1. Being so simple, it is a great way to learn and talk about lengths and angles. The center is put on a graph where the x axis and y axis cross, so we get this neat arrangement here. Sine, Cosine and Tangent
Chapter 5: Trigonometric Functions<BLURT>
Chapter 5: Trigonometric Functions 1. Please solve 2.
Algebra/Trig Review - Solving Trig Equations
Solve the following trig equations. For those without intervals listed find ALL possible solutions. For those with intervals listed find only the solutions that fall in those intervals.
Amplitude and Period
Amplitude and Period Learning Objective(s) · Understand amplitude and period. · Graph the sine function with changes in amplitude and period. · Graph the cosine function with changes in amplitude and period.
Section 4: Sine And Cosine Rule
These examples illustrate the decision-making process for a variety of triangles:
SOLVING TRIGONOMETRIC EQUATIONS
Note: If you would like an review of trigonometry, click on trigonometry. Solve for x in the following equation. Example 1: There are an infinite number of solutions to this problem. To solve for x, you must first isolate the sine term.