


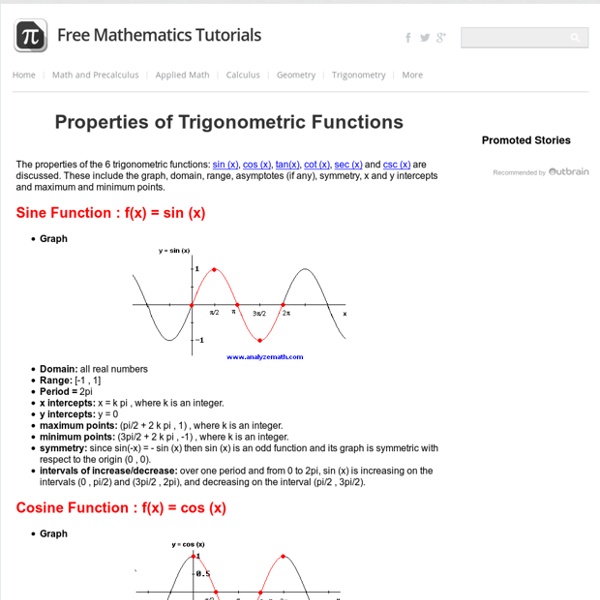
Basic Trigonometric Graphs Trigonometric Functions and Their Graphs: The Sine and Cosine (page 1 of 3) Sections: The sine and cosine, The tangent, The co-functions At first, trig ratios related only to right triangles. Then you learned how to find ratios for any angle, using all four quadrants. Then you learned about the unit circle, in which the value of the hypotenuse was always r = 1 so that sin(θ) = y and cos(θ) = x. Looking at the sine ratio in the four quadrants, we can take the input (the angle measure θ), "unwind" this from the unit circle, and put it on the horizontal axis of a standard graph in the x,y-plane. As you can see, the height of the red line, being the value of sin(θ) = y, is the same in each graph. If the green angle line had gone backwards, counting into negative angle measures, the horizontal graph on the right would have extended back to the left of zero. The Sine Wave When you do your sine graphs, don't try to plot loads of points. The Cosine Wave Top | 1 | 2 | 3 | Return to Index Next >>
Amplitude and Period Amplitude and Period Learning Objective(s) · Understand amplitude and period. · Graph the sine function with changes in amplitude and period. · Graph the cosine function with changes in amplitude and period. · Match a sine or cosine function to its graph and vice versa. You know how to graph the functions and . or , where a and b are constants. We used the variable previously to show an angle in standard position, and we also referred to the sine and cosine functions as . for the input (as well as to label the horizontal axis). . You know that the graphs of the sine and cosine functions have a pattern of hills and valleys that repeat. . (or ) on the interval looks like the graph on the interval . The graph below shows four repetitions of a pattern of length . is on the interval is one cycle. You know from graphing quadratic functions of the form that as you changed the value of a you changed the “width” of the graph. and see how changes to b will affect the graph. periodic, and if so, what is the period?
Amplitude, Period, Phase Shift and Frequency Some functions (like Sine and Cosine) repeat forever and are called Periodic Functions. The Period is the length from one peak to the next (or from any point to the next matching point): The Amplitude is the height from the center line to the peak (or to the trough). Or we can measure the height from highest to lowest points and divide that by 2. The Phase Shift is how far the function is horizontally to the right of the usual position. The Vertical Shift is how far the function is vertically from the usual position. All Together Now! We can have all of them in one equation: y = A sin(Bx + C) + D amplitude is A period is 2π/B phase shift is −C/B vertical shift is D Example: sin(x) This is the basic unchanged sine formula. So amplitude is 1, period is 2π, there is no phase shift or vertical shift: Example: 2 sin(4x − 2) + 3 amplitude A = 2 period 2π/B = 2π/4 = π/2 phase shift −C/B = −(−2)/4 = 1/2 vertical shift D = 3 In words: Note the Phase Shift formula −C/B has a minus sign: And we get: Frequency
Amplitude, Period and Frequency Learning Objectives Calculate the amplitude and period of a sine or cosine curve. Calculate the frequency of a sine or cosine wave. Graph transformations of sine and cosine waves involving changes in amplitude and period (frequency). Amplitude The amplitude of a wave is basically a measure of its height. , the wave is centered on the axis and the farthest away it gets (in either direction) from the axis is 1 unit. So the amplitude of (and ) is 1. Recall how to transform a linear function, like . value, you may remember that the slope of the graph affects the steepness of the line. The same is true of a parabolic function, such as , the graph would be either wider or narrower. , has the same parabolic shape but it has been “smooshed,” or looks wider, so that it increases or decreases at a lower rate than the graph of No matter the basic function; linear, parabolic, or trigonometric, the same principle holds. Look at the graphs of and Notice that the amplitude of is now 2. . Example 2: Graph . or . .
SOLVING TRIGONOMETRIC EQUATIONS Note: If you would like a review of trigonometry, click on trigonometry. Example 1: Solve for x in the following equation. There are an infinite number of solutions to this problem. First isolate the cosine term. To solve for x, we have to isolate x. Let's restrict the domain so the function is one-to-one on the restricted domain while preserving the original range. If we restrict the domain of the cosine function to that interval , we can take the arccosine of both sides of each equation. The angle x is the reference angle. Therefore, if , then The period of equals and the period of , this means other solutions exists every units. where n is an integer. The approximate values of these solutions are You can check each solution algebraically by substituting each solution in the original equation. You can also check the solutions graphically by graphing the function formed by subtracting the right side of the original equation from the left side of the original equation. Algebraic Check: Left Side:
Transformation of Trigonometric Graphs OML Search In these lessons, we will learn how Trigonometric Graphs can be transformed. the amplitude and vertical shift of Trigonometric Graphs the period and phase shift of Trigonometric Graphs Related Topics:More Trigonometric Lessons Stretching and Compressing of Graphs Amplitude of Trigonometric Functions The amplitude of a trigonometric function is the maximum displacement on the graph of that function. In the case of sin and cos functions, this value is the leading coefficient of the function. In the case of tan, cot, sec, and csc, the amplitude would be infinitely large regardless of the value of A. Period of Trigonometric Function The period of a function is the displacement of x at which the graph of the function begins to repeat. Consider y = sin x The value x = 2π is the point at which the graph begins to repeat that of the first quadrant. The general form isy = A sin Bxwhere is the amplitude and B determines the period. Solution: Since B = 2, the period is Solution: Rewrite Videos
Solving Trigonometric Equations Solving Trigonometric Equations (page 1 of 2) Solving trig equations use both the reference angles you've memorized and a lot of the algebra you've learned. Be prepared to need to think! Solve sin(x) + 2 = 3 for 0° < x < 360° Just as with linear equations, I'll first isolate the variable-containing term: sin(x) + 2 = 3 sin(x) = 1 Now I'll use the reference angles I've memorized: x = 90° Solve tan2(x) + 3 = 0 for 0° < x < 360° There's the temptation to quickly recall that the tangent of 60° involves the square root of 3 and slap down an answer, but this equation doesn't actually have a solution: tan2(x) = –3 How can the square of a trig function evaluate to a negative number? no solution Solve on 0° < x < 360° To solve this, I need to do some simple factoring: Now that I've done the algebra, I can do the trig. x = 30°, 90°, 270°, 330° Copyright © Elizabeth Stapel 2010-2011 All Rights Reserved Solve sin2(x) – sin(x) = 2 on 0° < x < 360° Only one of the factor solutions is sensible. x = 270° Hmm...
Solving Trigonometric Equations - She Loves Math This section covers: Solving trig equations is just finding the solutions of equations like we did with linear, quadratic, and radical equations, but using trig functions instead. We will mainly use the Unit Circle to find the exact solutions if we can, and we’ll start out by finding the solutions from We can also solve these using a Graphing Calculator, as we’ll see below. Important Note: there is a subtle distinction between finding inverse trig functions and solving for trig functions. for example, like in the The Inverse Trigonometric Functions section, we only pick the answers from Quadrants I and IV, so we get only. we get and in the interval (0, 2π); there are no domain restrictions. Let’s start out with solving fairly simple Trig Equations and getting the solutions from , or [0, 360°). Here is the Unit Circle again so we can “pick off” the answers from it: . is written as , and we can put it in the graphing calculator as or . and the right-hand side into and get the intersection.
The_trigonometry_functions Familiarity with the material in the modules, Introduction to Trigonometry and Further Trigonometry. Knowledge of basic coordinate geometry. Introductory graphs and functions. Facility with simple algebra, formulas and equations. In the module, Further Trigonometry, we saw how to use points on the unit circle to extend the definition of the trigonometric ratios to include obtuse angles. Once we can find the sine, cosine and tangent of any angle, we can use a table of values to plot the graphs of the functions y = sin x, y = cos x and y = tan x. The graphs of the sine and cosine functions are used to model wave motion and form the basis for applications ranging from tidal movement to signal processing which is fundamental in modern telecommunications and radio-astronomy. Angles in the four quadrants Redefining the Trigonometric Ratios We begin by taking the circle of radius 1, centre the origin, in the plane. We mark the angle POQ as θ. (cos θ, sin θ). For acute angles, we know that tan θ = a
Exploring y=Asin(Bx+C)+D Assignment 1: Exploring Asin(Bx+C)+D by Margo Gonterman Periodic Function A periodic function is a function, such as sin(x), that repeats its values in regular intervals Sin(x) oscillates, or goes back and forth, between its maximum and minimum value Amplitude The amplitude of the graph is the maximum height the graph reaches from the x-axis Period The period is the distance along the x-axis that is required for the function to make one full oscillation Phase Shift The phase shift is the measure of how far the graph has shifted horizontally Vertical Shift The vertical shift is the measure of how far the graph has shifted vertically, either up or down, from its initial position Let's examine the graph of y=sin(x). The graph of y=sin(x) has: - an amplitude of 1 - a period of 2pi - a phase shift of 0 - a vertical shift of 0 Let's look at what happens as A varies When A=1, the graph has an amplitude of 1. As A increases increases from 1, the amplitude of the graph increases. The period of the graph is |(2pi)/B|.
Trigonometry Trigonometry (from Greek trigonon "triangle" + metron "measure") Want to Learn Trigonometry? Here is a quick summary. Follow the links for more, or go to Trigonometry Index Right Angled Triangle The triangle of most interest is the right-angled triangle. The right angle is shown by the little box in the corner. We usually know another angle θ. And we give names to each side: Adjacent is adjacent (next to) to the angle θ Opposite is opposite the angle θ the longest side is the Hypotenuse "Sine, Cosine and Tangent" Trigonometry is good at find a missing side or angle in a triangle. The special functions Sine, Cosine and Tangenthelp us! They are simply one side of a right-angled triangle divided by another. For any angle "θ": (Sine, Cosine and Tangent are often abbreviated to sin, cos and tan.) Example: What is the sine of 35°? Calculators have sin, cos and tan, let's see how to use them: Example: What is the missing length here? We know the Hypotenuse We want to know the Opposite sin(45°) = 0.7071...