

Ouvert (topologie) Il existe plusieurs définitions des ouverts suivant le type d'espace concerné.
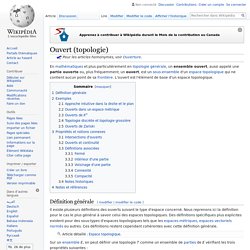
Nous reprenons ici la définition pour le cas le plus général à savoir celui des espaces topologiques. Des définitions spécifiques plus explicites existent pour des sous-types d'espaces topologiques tels que les espaces métriques, espaces vectoriels normés ou autres. Ces définitions restent cependant cohérentes avec cette définition générale. Sur un ensemble E, on peut définir une topologie T comme un ensemble de parties de E vérifiant les trois propriétés suivantes : Alors par définition un sous-ensemble U de E est un ouvert de E pour la topologie T si et seulement si U appartient à T (il en résulte que la topologie T peut être définie comme l'ensemble des ouverts de E selon T). Les espaces topologiques les plus couramment étudiés sont munis de diverses structures supplémentaires : Exemple : Les points (x, y) qui satisfont à l'équation x2 + y2 = r2 sont en bleu. Exemple Contre-exemple. Bouteille de Klein.
Un article de Wikipédia, l'encyclopédie libre. vue de la bouteille de Klein dans un espace à trois dimensions.
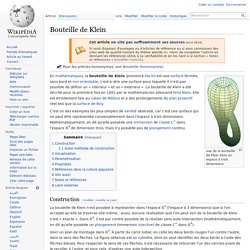
Construction[modifier | modifier le code] Voici un plan de montage dans ℝ3. À partir du carré initial, on colle les deux bords rouges l'un contre l'autre, dans le sens des flèches. La figure obtenue est un cylindre, dont on veut identifier les deux bords à l'aide des flèches bleues. Si les deux segments bleus étaient orientés de la même façon, le recollement des segments opposés donnerait un tore. Autre méthode de construction[modifier | modifier le code] La bouteille de Klein peut aussi être obtenue par recollement de deux rubans de Möbius le long de leurs bords. On se donne deux exemplaires d'un tel carré, et on obtient deux exemplaires de ruban de Möbius en faisant cette fois d'abord l'identification suivant les flèches bleues.
Variété (géométrie) Un article de Wikipédia, l'encyclopédie libre.
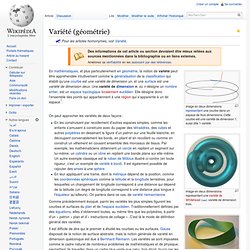
Pour les articles homonymes, voir Variété. Image en deux dimensions représentant une courbe dans un espace de trois dimensions. Cette courbe est une variété de dimension 1, aussi dite 1-variété. Réalisation du ruban de Möbius à partir du collage d'une bande de papier. Le « bord » n'est que d'un seul tenant. Variétés. Professeur, Université Lille 1.

Responsable de notre rubrique Café des maths. (page web) Un jour, lorsque je m’apprêtais à descendre de l’autobus, une dame qui était à côté de moi me demanda : « S’il-vous-plaît, qu’est-ce que c’est qu’une variété ? » Comme les portes s’ouvraient, je répondis de manière extrêmement concise : « Vous voyez ce qu’est une surface, par exemple une feuille de salade ?
Je ne sais pas ce que la dame a pu comprendre de cette description. Mais tout d’abord, pourquoi m’a-t-elle posé cette question ? Pourquoi faut-il généraliser la notion de surface de l’espace « physique » quotidien en dimension quelconque ? Les concepts de grandeur ne sont possibles que là où il existe un concept général qui permette différents modes de détermination. Pour plus de détails sur le contexte de cet article, on pourra consulter le billet du 18 Octobre 2009 de Joël Merker, intitulé « Assembler l’inachevé ». Topologie - 4e ed. - Cours et exercices corrigés - Hervé Queffélec. Topologie générale: Chapitres 1 à 4 - N. Bourbaki. Experiments in Topology - Stephen Barr. Topologie de la droite réelle. Un article de Wikipédia, l'encyclopédie libre.
Richard Dedekind (1831 - 1916) a défini rigoureusement les nombres réels et posé les bases de leur étude topologique. partir des propriétés de l'ensemble des nombres réels pour définir les objets de la topologie ;partir des axiomes de la topologie générale et les appliquer à l'ensemble des nombres réels. La topologie de la droite réelle est une topologie de l'ordre et l'ensemble des nombres réels est un corps topologique, ce qui signifie que les notions de limite et de continuité sont compatibles avec l'ordre et les opérations usuelles (addition, soustraction, multiplication et division autre que la division par zéro). Construction et topologie de la droite réelle[modifier | modifier le code] Insuffisance et complétion des nombres rationnels[modifier | modifier le code] si x ≤ y, alors x+a ≤ y+a et si x ≤ y et a > 0, alors a x ≤ a y. x0 = 1 xn+1 = xn/2 +1/xn Deux suites de Cauchy sont dites équivalentes lorsque leur différence tend vers zéro.
Ou.