

Which Mistake Most Surprises You? « Math Mistakes. Fraction comparison for 4th Graders.
They’ve been working a lot with representing fractions as circles and as rectangles. They’ve done some basic addition with fractions. Most aren’t generally able to find equivalent fractions. What mistakes do you expect to see in the class set? Guinness World Record – The largest popsicle stick chain reaction. Guinness World Record – The largest popsicle stick chain reaction. Inside mathematics - a professional resource for educators / Polya. George Polya was a Hungarian who immigrated to the United States in 1940.

His major contribution is for his work in problem solving. Growing up he was very frustrated with the practice of having to regularly memorize information. He was an excellent problem solver. Relief Teaching Ideas. A game for 2 or 3 players.

Each player chooses a colour pencil or texta they will use in the game. Players take turns rolling the dice, using the numbers that they rolled to draw the perimeter of a rectangle or square & writing the area in the middle of the shape. Game ends when players run out of room to draw. Winner is the player who has used the largest area/most squares.
This game is an old favourite. Second Grade Math Japanese Lesson Study. Lesson study in japan. Max Ray at NCTM Ignite. Browse Talks. Gesturing with hands is a powerful tool for children’s math learning. Children who use their hands to gesture during a math lesson gain a deep understanding of the problems they are taught, according to new research from the University of Chicago’s Department of Psychology.
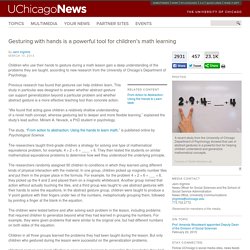
Previous research has found that gestures can help children learn. This study in particular was designed to answer whether abstract gesture can support generalization beyond a particular problem and whether abstract gesture is a more effective teaching tool than concrete action. “We found that acting gave children a relatively shallow understanding of a novel math concept, whereas gesturing led to deeper and more flexible learning,” explained the study’s lead author, Miriam A. Novack, a PhD student in psychology. The study, “From action to abstraction: Using the hands to learn math,” is published online by Psychological Science.
The researchers taught third-grade children a strategy for solving one type of mathematical equivalence problem, for example, 4 + 2 + 6 = ____ + 6. Tips For Teachers On Using Digital Technology. Geometry Is Worth The Extra Time… As I am sure many teachers can attest, there is a constant struggle each year between covering content and the precious amount of time we have to engage the students in learning.
Prior to the past two years in the classroom, this guilt always seemed to creep up most during our geometry units. I used to feel that once the students could find area, perimeter, and volume, we would move back into our fraction and decimal work because that always took SO much time to develop a deep, foundational understanding. While geometric representations such as an area model support the fraction and decimal work, it is still not the 2D or 3D unit work. Alyssa and India.. Productive struggle and aha moment.
TEDxTeen - Jacob Barnett: Forget What You Know. First grade equality sign misconception. Cube Nets. Coin Box. Math Conversations that Count: Grades 1 to 12 - LearnTeachLead.caLearnTeachLead.ca. Geometry Is Worth The Extra Time… Deux problèmes du carrefour - Google Slides. Google Slides - create and edit presentations online, for free. Gratte-ciels - Presentaciones de Google. Conceptis logic puzzles - Have fun, get smart! Www.nelson.com/linearrelationships/From Patterns to Algebra Sampler 2012.pdf. From%20Patterns%20to%20Algebra%20Sampler%202012.pdf. Quick Draw - The problem-centered classroom - Problem centered math. All meaningful mathematics learning is imaged-based.
While there may be certain forms of mathematical reasoning that seem not to use imagery, most mathematical activity has a spatial component. If school mathematics is procedural, students may fail to develop their capacity to form mental images of mathematical patterns and relationships. It is well documented that students who reason from images tend to be powerful mathematics students. Further, we know that the ability to use images effectively in doing mathematics can be developed. When students are encouraged to develop mental images and use those images in mathematics, they show surprising growth. Quick Draw is an engaging mathematical activity that helps students develop their mental imagery.
The discussion of what they saw is a crucial component of the activity. Quick Draw activities Two sample activities appear below. Watch the video. Inspiring Students to Math Success and a Growth Mindset. Cathy Bruce sur Twitter : "What fraction of this design is red? more challenging? If the blue triangle is worth 1. What is whole design worth? L'enquête collaborative. ETFO Pley. Moutons. CAMI. Coplanification-RR février2015. Falling+origami+papers.jpg (1334×1600) Chopsticks.jpg (JPEG Image, 1600 × 1600 pixels) - Scaled (62%) Developingthequestion. From Pearson’s Common Core Algebra 2 text (and everyone else’s Algebra 2 text for that matter): Mark has 42 coins consisting of dimes and quarters.
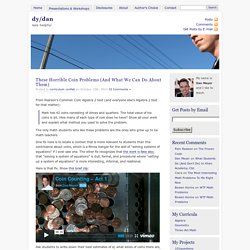
The total value of his coins is $6. How many of each type of coin does he have? Show all your work and explain what method you used to solve the problem. The only math students who like these problems are the ones who grow up to be math teachers. [Mathématiquement vôtre] Référentiel pour l'enseignement des angles... - jjcp20002000 - Gmail. A Learning Community. Steve Leinwand. It’s been a great fall of 2014 – many states, many schools and many classrooms.
It’s been full of hope and optimism as I see many positive aspects of the Common Core era, more and better use of the incredible array of new on-line resources (see: ), and powerful forays into effective collaboration and coaching. But then there was a discouraging return to reality. I’m in a majority minority suburban school district with more than 12,000 students working with middle and high school teachers about strengthening the teaching and learning of algebra, and it’s the typical one-day one-shot PD. I returned to the airport consumed by the question of HOW DO WE HAVE THE AUDACITY TO BLAME TEACHERS when: Steve Wyborney's Blog: I'm on a Learning Mission.
Trent Mathematics Education Research Collaborative. Bruce_Yearley_OAMELeadershipNov2014.pdf - Google Drive. Number Balance. Full Screen Version This is a number balance.
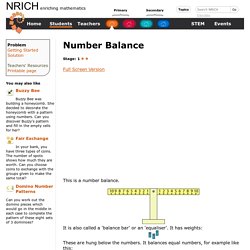
It is also called a 'balance bar' or an 'equaliser'. It has weights: These are hung below the numbers. Visual Patterns - 1-20. OAME Leadership 2014 « Amy Lin. 1001 Math Problems. YouCubed - Join the Revolution. Jo Boaler. Words I Want To Hear More In My Classroom. Today, I present to you: Words I Want To Hear More In My Classroom I decided if these words are that important to me, they need to be on display in my classroom as a reminder to myself and to my students.
So, I decided to make a few posters of these words to hang in my classroom. Harry Wong emphasizes the importance of using please and thank you in your conversations with students in his book The First Days of School: How to Be an Effective Teacher . A Passion for Math: Elly Schofield at TEDxClaremontColleges. Celine RC sur Twitter : "Surface d'écriture verticale, non-permanente - minileçon avec vue sur la neige... Touch Count - Faculty of Education. Tangible Mathematics for the iPad This project involves the development of applications for the iPad that are focused on early number sense. This site provides an overview of the current application, information for Field Testers and Task ideas for teachers and parents.
Background Information Current mathematics education software has been developed for the desktop/laptop paradigm of technology use where the mouse and keyboard are essential interfaces. Even software for interactive whiteboards (IWBs) does not take full advantage of touch-screen capacities because the mouse/keyboard interface is the default interaction mode. The touch-screen iPads also enable a much more intuitive interface suitable for young learners, allowing them to use their fingers and gestures to explore mathematics ideas and express mathematical understandings. Wp-content/uploads/2014/09/Jo-Boaler-transcripts.pdf. Showbie - The paperless classroom made simple. Asking students to choose their own path and justify it. Showbie for ipad. Vertical Non-Permanent Surfaces and Visible Random Groupings. I presented these ideas at Twitter Math Camp 14 in the flex session on Saturday afternoon. Let me be clear, these great ideas belong to Peter Liljedahl and he deserves all the praise.
I was fortunate to be asked to present at the Canadian Mathematics Education Forum about spiralling the curriculum with activity based teaching. This is where Peter was a Keynote speaker. His idea of visible random groupings (VRG) and Vertical Non-Permanent Surfaces (VNPS) resonated with me. I felt it was an excellent teacher move to increase engagement in my classroom and to have learning be student centered. This post will probably be a little long as I would like to include some of his research as well. Visibly random groups & Vertical non-permanent surfaces. I have been trying to shift my Math classes toward activity- / problem-based learning. We still have individual practice days, but as much as possible I want them solving new, complicated problems in groups.
Two ideas that I heard about at a meeting of the OCDSB Mathematics Department Heads have really changed how I do things in class lately: Visibly Random GroupsVertical Non-Permanent Surfaces Both ideas come from the work of Peter Liljedahl and have been gaining traction amongst OCDSB teachers lately, particularly in Mathematics classrooms. Visibly Random Groups (VRGs): Every day I make random groups so that my students work with different partners each day. #edcampottawa Session One: Alternatives to Paper and Pencil Testing &Session Two:Turning Points in Assessment. Bit of a ramble in this post as I wrote it live.
Everything in this post is not thought out, everything in this post is not my thoughts, everything in this post is what I heard or said at #edcampottawa, everything is not linear (ideas are as they were heard), everything in this post is the collective of #edcampottawa. Have fun reading this. My apologies to everyone that was there as I was doing this (typing slowly) instead of truly engaging. Lionel. Visibly random groups & Vertical non-permanent surfaces. Conversations mathématiques. A Passion for Math: Elly Schofield at TEDxClaremontColleges. Parent Influence & Social Modeling in Math. Mon disque - Google Disque. Réseau et Stratégie numératie - Google Présentations. Open Middle - Challenging math problems worth solving. Robert Kaplinsky - Glenrock Consulting. Robert Kaplinsky - Glenrock Consulting.
I have seen quite a few posters to describe Webb’s Depth of Knowledge but I recently came across a set that is now my favorite. In particular, I love the bullet point lists that explain each of the levels as I believe that focusing on the verbs can lead to confusion (for example, “explain” can be level 1 through 4 depending on how it is used). Click the “Download Files” to download two PDFs: one has all four levels on a single sheetone has each level on its own sheet in a bigger size I got these posters via Alyda Mir who got them from Linda Evans. If you know who the posters were originally created by, please let me know so I can give proper attribution. Download Files. Robert Kaplinsky - Glenrock Consulting. The Situation You are hosting a barbeque that starts very soon and you want to make as many biscuits as possible with the ingredients you already have.
The Challenge(s) Questioning My Metacognition. Check out Dan’s Blog or watch Math Class Needs a Makeover ***click here for the question and big idea of each task *** Open Middle - Challenging math problems worth solving. Make a math video. Sylvie Levasseur (@SylvieLL) Conrad Wolfram: Teaching kids real math with computers.
Galerie des stratégies - Barres de Singapour - Google Slides. SlamDunkMath. Ressources internet et articles intéressants. Asking students to choose their own path and justify it. Home Page. Teachers Primary Pupils. Nrich.maths.org/content/id/4348/cuisenaire.swf. Estimation 180 - Home. Contexts for Learning Mathematics - DreamBox Learning. I’m Cathy Fosnot, I was a professor for many years at City College of New York, I founded the Mathematics in the City, a National Centre of in-service for Math education and the author of various books and articles on mathematics education including the Contexts for Learning Series from Heinemann, and I am the Senior Content Advisor with the academic team in DreamBox learning. When children are constructing multiplication they often start by needing to build a whole system of ones. So, if the context is “What’s 3 x 6?” Cathy Fosnot - Doing Computations with Understanding.
Cathy Fosnot - Doing Computations with Understanding. Cathy Fosnot - Why is Numeracy Important. WMC 2014 Conference Ignite Session - Cathy Fosnot. Cathy Fosnot - What is Numeracy? Finding Ways. La guerre des maths. Play KenKen Math Puzzles - Free Math Games & Logic Puzzles! 1001 Visual Puzzles. 1001 Math Problems. 10 classroom routines that get kids talking (and writing) about math strategies. 21st Century Fluencies: Make a Math Video. 21st Century Fluencies: Scale Models in Math.