

Www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_RESOURCE/U10_L2_T1_text_container.html. 101 uses of a quadratic equation. March 2004 It isn't often that a mathematical equation makes the national press, far less popular radio, or most astonishingly of all, is the subject of a debate in the UK parliament.

Everyday Examples of Situations to Apply Quadratic Equations. Binary Game. Skip to Content | Skip to Footer Cisco Binary Game The Cisco Binary Game is the best way to learn and practice the binary number system.
It is great for classes, students and teachers in science, math, digital electronics, computers, programming, logic and networking. Binary, Decimal and Hexadecimal Numbers. Decimals To understand Binary and Hexadecimal numbers, it is best to know how Decimal Numbers work.

Every digit in a decimal number has a "position", and the decimal point helps us to know which position is which. The position just to the left of the point is the "Units" position. Every position further to the left is 10 times bigger, and every position further to the right is 10 times smaller: Computational Thinking Toolkit. Exploring Computational Thinking. Csta.acm.org/Curriculum/sub/CurrFiles/472.11CTTeacherResources_2ed-SP-vF.pdf. Math Games and Puzzles. Parabola. Try kicking the ball: © 2016 MathsIsFun.com v0.88 Definition A parabola is a curve where any point is at an equal distance from: a fixed point (the focus ), and a fixed straight line (the directrix ) Get a piece of paper, draw a straight line on it, then make a big dot for the focus (not on the line!).
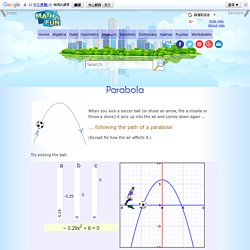
Now play around with some measurements until you have another dot that is exactly the same distance from the focus and the straight line. Keep going until you have lots of little dots, then join the little dots and you will have a parabola! Names Here are the important names: Drawing. This tutorial is for Processing version 1.1+.

If you see any errors or have comments, please let us know. This tutorial is from the book, Learning Processing, by Daniel Shiffman, published by Morgan Kaufmann Publishers, Copyright 2008 Elsevier Inc. Starter kit of components. Logic Gates Part 1 (With Simulator!) Fundamentals of Data Representation: Binary fractions. So far we have only looked at whole numbers (integers), we need to understand how computer represent fractions.
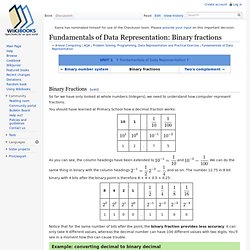
You should have learned at Primary School how a decimal fraction works: As you can see, the column headings have been extended to. Ms. Computer Teacher - Ms. Computer Teacher. An Introduction To Digital Electronics: The Intro - PyroEDU. Basic Logic Gates. Logic Puzzles. Gyu.people.wm.edu/Fall2012/Fall2012-math214/truth.table.puzzle.problem.pdf. The Ultimate Puzzle Site - Logical Puzzles. A rather silly car thief stole, without knowing it, the car of the chief of police.
The police immediately started an investigation and based on witness depositions, four suspects were arrested that were seen near the car at the time of the crime. Because the chief of police took the case very seriously, he decided to examine the suspects personally and use the new lie detector of the police station. Each suspect gave three statements during the examinations, which are listed below: Introduction to algebra. How to fit a quadratic Equation using Excel. 101 uses of a quadratic equation. Quadratic Equations. An example of a Quadratic Equation: The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x2).

Content, standard-form. Standard form is a way of writing down very large or very small numbers easily. 103 = 1000, so 4 × 103 = 4000 .
So 4000 can be written as 4 × 10³ . This idea can be used to write even larger numbers down easily in standard form. Small numbers can also be written in standard form. However, instead of the index being positive (in the above example, the index was 3), it will be negative. Computer science. Computer representation of numbers. Computers store numbers in a variety of ways, but all use base-2 arithmetic, rather than our base 10.

Almost all computers bits in multiples of 8 to store numbers; one units of 8 bits is called a byte. There are two main ways to represent numbers: integer and floating point. Integer representation Suppose we consider positive integers only. What range of values can we represent with a single byte? Online Courses from the World's Experts. Computational Thinking - IAE-Pedia. Information Age Education (IAE) is an Oregon non-profit corporation created by David Moursund in July, 2007. It works to improve the informal and formal education of people of all ages throughout the world. A number of people have contributed their time and expertise in developing the materials that are made available free in the various IAE publications.
Click here to learn how you can help develop new IAE materials. Computers are incredibly fast, accurate, and stupid. Human beings are incredibly slow, inaccurate, and brilliant. Introduction. Www.iste.org/docs/learning-and-leading-docs/march-2011-computational-thinking-ll386.pdf. Computational Thinking by Busra Zorba.
Computational Thinking: A Digital Age Skill for Everyone. The Logic Lab: simulating simple circuits of logic gates. Logic Gate Simulator. Digital Circuits/Adders. Half Adder [ edit ] Consider adding two binary numbers together: The Base-2 System and the 8-bit Byte" The reason computers use the base-2 system is because it makes it a lot easier to implement them with current electronic technology. You could wire up and build computers that operate in base-10, but they would be fiendishly expensive right now.
On the other hand, base-2 computers are relatively cheap. So computers use binary numbers, and therefore use binary digits in place of decimal digits. The word bit is a shortening of the words "Binary digIT. " Whereas decimal digits have 10 possible values ranging from 0 to 9, bits have only two possible values: 0 and 1. Simple Gates" CHAPTER 8 — Binary Addition and Two's Complement.
A Level Computing OCR exam board - Twos Complement - 2's complement. Math of Vector Art. Computational Thinking. Sites/default/files/activity_pdfs_full/unpluggedTeachersMar2010-USletter.pdf. Computational thinking. Exploring Computational Thinking. Computational thinking (CT) involves a set of problem-solving skills and techniques that software engineers use to write programs that underlie the computer applications you use such as search, email, and maps.
However, computational thinking is applicable to nearly any subject. Students who learn computational thinking across the curriculum begin to see a relationship between different subjects as well as between school and life outside of the classroom. Specific computational thinking techniques include: problem decomposition, pattern recognition, pattern generalization to define abstractions or models, algorithm design, and data analysis and visualization. Decomposition: The ability to break down a task into minute details so that we can clearly explain a process to another person or to a computer, or even to just write notes for ourselves. Decomposing a problem frequently leads to pattern recognition and generalization, and thus the ability to design an algorithm.