

LABORES for the Natural and Digital Sciences. Ray Toal. Books Ray Toal, Rachel Rivera, Alex Schneider, and Eileen Choe, Programming Language Explorations, CRC Press, 2017.

John David N.
Automata. Research. Computational complexity theory. Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other.
A computational problem is understood to be a task that is in principle amenable to being solved by a computer, which is equivalent to stating that the problem may be solved by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying the amount of resources needed to solve them, such as time and storage.
Modular Arithmetic. Quaternary. Ternary. Low Complexity. Discrete. Super-recursive algorithm. Malament–Hogarth spacetime. A Malament–Hogarth (M-H) spacetime, named after David B.
Malament and Mark Hogarth, is a relativistic spacetime that possesses the following property: there exists a worldline and an event such that all events along are a finite interval in the past of , but the proper time along is infinite. Is known as an M-H event. 's past to set a computer (Turing machine) to work on some task and then have the Turing machine travel on , computing for all eternity.
Hermite polynomials. In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; in finite element methods as shape functions for beams; and in physics, where they give rise to the eigenstates of the quantum harmonic oscillator.
They are also used in systems theory in connection with nonlinear operations on Gaussian noise. They are named after Charles Hermite (1864)[1] although they were studied earlier by Laplace (1810) and Chebyshev (1859).[2] Definition[edit] Umbral calculus. In mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them.
These techniques were introduced by John Blissard (1861) and are sometimes called Blissard's symbolic method. They are often attributed to Édouard Lucas (or James Joseph Sylvester), who used the technique extensively.[1] In the 1930s and 1940s, Eric Temple Bell attempted to set the umbral calculus on a rigorous footing. In the 1970s, Steven Roman, Gian-Carlo Rota, and others developed the umbral calculus by means of linear functionals on spaces of polynomials. Currently, umbral calculus refers to the study of Sheffer sequences, including polynomial sequences of binomial type and Appell sequences, but may encompass in its penumbra systematic correspondence techniques of the calculus of finite differences.
The 19th-century umbral calculus[edit] An example involves the Bernoulli polynomials. ATLAS of Finite Group Representations - V3. P versus NP problem. Diagram of complexity classes provided that P≠NP.
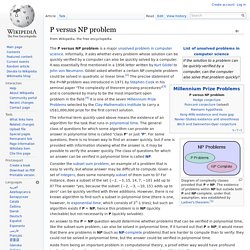
The existence of problems within NP but outside both P and NP-complete, under that assumption, was established by Ladner's theorem.[1] The P versus NP problem is a major unsolved problem in computer science. Informally, it asks whether every problem whose solution can be quickly verified by a computer can also be quickly solved by a computer. It was essentially first mentioned in a 1956 letter written by Kurt Gödel to John von Neumann. Gödel asked whether a certain NP complete problem could be solved in quadratic or linear time.[2] The precise statement of the P=NP problem was introduced in 1971 by Stephen Cook in his seminal paper "The complexity of theorem proving procedures"[3] and is considered by many to be the most important open problem in the field.[4] It is one of the seven Millennium Prize Problems selected by the Clay Mathematics Institute to carry a US$1,000,000 prize for the first correct solution. Context[edit] Gödel’s Lost Letter and P=NP.
Combinatorial Game Theory. Combinatorial Game Theory studies strategies and mathematics of two-player games of perfect knowledge such as chess or go (but often either concentrating instead on simpler games such as nim, or solving endgames and other special cases).

An important distinction between this subject and classical game theory (a branch of economics) is that game players are assumed to move in sequence rather than simultanously, so there is no point in randomization or other information-hiding strategies. The bible of combinatorial game theory is Winning Ways for your Mathematical Plays, by E. R. Berlekamp, J. H. Recent additions: Older stuff: Abstract Games Magazine Akron, connection game similar to hex but based on stacking balls in 3d over a square lattice. David Eppstein, Dept. Www.pelulamu.net/binmyst/ Title: The Mystery of the Binary Author: Viznut Originally published in the [ALT] magazine issue 0x0000 The subcultures of computing are very young.

There are no legends nor values that come from the distant past. No ancient mysticism, no generations-old symbols that have deep emotional effects. Even the old and classical things tend to be quite recent. Fortunately, even the past is not static. Stone-age binary counting.