

Xiaolin Wu's line algorithm. Xiaolin Wu's line algorithm You are encouraged to solve this task according to the task description, using any language you may know.
Wu Anti-aliased Lines. Bresenham. Bresenham. The Beauty of Bresenham's Algorithm A simple implementation to plot lines, circles, ellipses and Bézier curves.

The Algorithm This page introduces a compact and efficient implementation of Bresenham's algorithm to plot lines, circles, ellipses and Bézier curves. A detailed documentation of the algorithm and more program examples are availble in PDF: Bresenham.pdf. Some C-program examples of the document are listed below. GitHub - dbousque/fdf-generator: Convert a BMP image into a fdf file. FDF Map Generator. AL7MA20TEPA0111 Sequence 05. AL7MA20TEPA0111 Sequence 02.
AL4MA51TEWB1116 Espace Geometrie. Algorithme de tracé de segment de Bresenham. L’algorithme de tracé de segment de Bresenham est un algorithme développé par Jack E.
Bresenham en mai 1962, alors qu’il travaillait dans un laboratoire informatique d’IBM et cherchait à piloter un traceur attaché à une console texte. Cet algorithme a été présenté à la convention de l’ACM en 1963, puis publié en 1965 dans la revue IBM Systems Journal. L’algorithme détermine quels sont les points d’un plan discret qui doivent être tracés afin de former une approximation de segment de droite entre deux points donnés.
Cet algorithme est souvent utilisé pour dessiner des segments de droites sur l’écran d’un ordinateur ou une image calculée pour l’impression. Il est considéré comme l’un des premiers algorithmes découverts dans le domaine de la synthèse d'image. Utilisations[modifier | modifier le code] L’algorithme est également facilement adaptable au calcul de courbes et surfaces dans un espace discret de plus de 2 dimensions (notamment pour le pilotage de machines outils). , la rangée. Tutoriel 12 - Projection en perspective. Nous avons enfin atteint l'élément qui représente le mieux les graphismes 3D : la projection du monde 3D au monde 2D tout en maintenant l'impression de profondeur.
Un bon exemple est l'image d'une route ou d'un rail de chemin de fer qui converge vers un point distant à l'horizon. Nous allons générer la transformation qui satisfait les contraintes ci-dessus et une contrainte supplémentaire : nous allons rendre la vie plus facile au clipper en représentant les coordonnées projetées dans l'espace normalisé de -1 à +1. Cela signifie que le clipper peut faire son travail sans avoir connaissance ni des dimensions de l'écran, ni de la position des plans Z (plan Z proche et plan Z lointain). La transformation de projection en perspective va nous imposer de fournir quatre paramètres : Matrice projection perspective. Perspective axonométrique. Un article de Wikipédia, l'encyclopédie libre.
En dessin technique et en architecture, une perspective parallèle, ou perspective cylindrique ou perspective axonométrique est une forme de représentation en deux dimensions d'objets en trois dimensions qui a pour objectif de conserver l'impression de volume ou de relief. Appelée aussi parfois perspective rapide ou perspective artificielle, elle est différente de la perspective conique et ne représente pas ce que l’œil voit réellement : en particulier les parallèles restent représentées par des parallèles et les distances ne sont pas réduites par l'éloignement. Perspective isométrique. Arche en perspective isométrique.
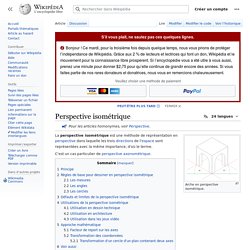
C'est un cas particulier de perspective axonométrique. Principe[modifier | modifier le code] Cube vu en perspective isométrique. En géométrie analytique, on définit un repère orthonormé. La perspective isométrique correspond à une vue selon la droite de vecteur directeur (1, 1, 1) dans ce repère. Perspective cavalière. Untitled. Algorithmique de base de l'Infographie. Dessin 2D des objets de base Algorithmes de tracé de segments Algorithme de base pour beaucoup de traitements de l'Informatique Graphique: Dessin en fil de fer Remplissage Elimination des parties cachées ...

Cet algorithme doit être efficace car "mis à toutes les sauces". On désire tracer un segment entre deux points (xi,yi) et (xf,yf) de R2. Ce tracé est effectué sur un écran bitmap (composé d'une matrice de n x m pixels carrés). -> Le segment doit être discrétisé (rasterisé). Problème: Quels pixels doit-on tracer? Trois impératifs: Isometric Tiles Math. Working with isometric tiles is a bit trickier than a plain square grid.

This tutorial is for beginner game programmers looking to wrap their heads around isometric math. Instead of simply handing you formulas, I intend to explain what they do and how they should be used. There are many ways of handling isometric tiles but we're only going to talk about one method. This happens to be the most commonly used method. It's the way that isometry is handled in the Tiled map editor, so it's definitely a good approach if you want to use that tool.
Orthographic Projection When working in isometric project, your maps will still be a simple 2D array (or equivalent) in memory -- just as if you were working in a simpler orthographic projection (e.g. side or top view). Our grid in "map" coordinates -- how our array looks in memory, Values are (map.x, map.y)
Scratchapixel. Rastérisation. Un article de Wikipédia, l'encyclopédie libre.
La rastérisation, ou matricialisation, est un procédé qui consiste à convertir une image vectorielle en une image matricielle destinée à être affichée sur un écran ou imprimée par un matériel d'impression. Les scènes en 3 dimensions étant généralement stockées en mémoire de manière vectorielle, ce terme s'applique également pour leur rendu à l'écran (l'écran fournissant une image matricielle), c'est d'ailleurs la principale utilisation du mot « rastérisation ».
Par extension, on englobe aussi dans la rastérisation tous les procédés permettant d'améliorer l'aspect final du rendu 3D. La rastérisation d'images en deux dimensions étant nécessaire à l'intérieur de son équivalent 3D, la suite de cet article s'intéressera uniquement à la rastérisation d'images en trois dimensions dans le but de détailler les deux méthodes simultanément.
Étymologie[modifier | modifier le code]