

John F. Nash, Jr. - Autobiography. My beginning as a legally recognized individual occurred on June 13, 1928 in Bluefield, West Virginia, in the Bluefield Sanitarium, a hospital that no longer exists.
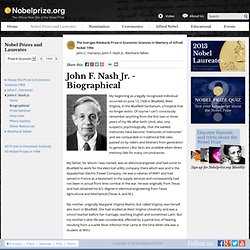
Of course I can't consciously remember anything from the first two or three years of my life after birth. (And, also, one suspects, psychologically, that the earliest memories have become "memories of memories" and are comparable to traditional folk tales passed on by tellers and listeners from generation to generation.) But facts are available when direct memory fails for many circumstances. My father, for whom I was named, was an electrical engineer and had come to Bluefield to work for the electrical utility company there which was and is the Appalachian Electric Power Company. He was a veteran of WW1 and had served in France as a lieutenant in the supply services and consequently had not been in actual front lines combat in the war. I also did electrical and chemistry experiments at that time. Thus further time passed. Solving Fermat: Andrew Wiles. Posted 11.01.00 NOVA Andrew Wiles devoted much of his career to proving Fermat's Last Theorem, a challenge that perplexed the best minds in mathematics for 300 years.
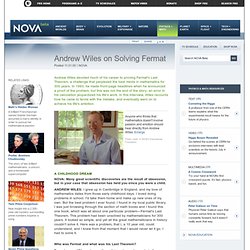
In 1993, he made front-page headlines when he announced a proof of the problem, but this was not the end of the story; an error in his calculation jeopardized his life's work. In this interview, Wiles recounts how he came to terms with the mistake, and eventually went on to achieve his life's ambition. Anyone who thinks that mathematics doesn't involve passion and emotion should hear directly from Andrew Wiles. Enlarge Photo credit: © WGBH Educational Foundation A childhood dream NOVA: Many great scientific discoveries are the result of obsession, but in your case that obsession has held you since you were a child. Évariste Galois. Life[edit] Early life[edit] Galois was born on 25 October 1811 to Nicolas-Gabriel Galois and Adélaïde-Marie (born Demante).
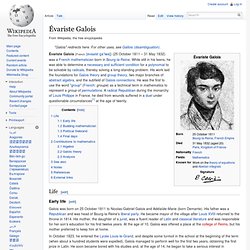
His father was a Republican and was head of Bourg-la-Reine's liberal party. He became mayor of the village after Louis XVIII returned to the throne in 1814. His mother, the daughter of a jurist, was a fluent reader of Latin and classical literature and was responsible for her son's education for his first twelve years. In October 1823, he entered the Lycée Louis-le-Grand, and despite some turmoil in the school at the beginning of the term (when about a hundred students were expelled), Galois managed to perform well for the first two years, obtaining the first prize in Latin. He found a copy of Adrien Marie Legendre's Éléments de Géométrie, which it is said that he read "like a novel" and mastered at the first reading.
Srinivasa Ramanujan. Srinivasa Ramanujan Iyengar FRS (pronunciation: i/sriː.ni.vaː.sə raː.maː.nʊ.dʒən/) (22 December 1887 – 26 April 1920) was an Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series, and continued fractions.
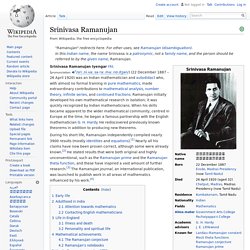
Ramanujan initially developed his own mathematical research in isolation; it was quickly recognized by Indian mathematicians. When his skills became apparent to the wider mathematical community, centred in Europe at the time, he began a famous partnership with the English mathematician G. H. Hardy. Carl Friedrich Gauss. Johann Carl Friedrich Gauss (/ɡaʊs/; German: Gauß, pronounced [ɡaʊs]; Latin: Carolus Fridericus Gauss) (30 April 1777 – 23 February 1855) was a German mathematician who contributed significantly to many fields, including number theory, algebra, statistics, analysis, differential geometry, geodesy, geophysics, mechanics, electrostatics, astronomy, matrix theory, and optics.
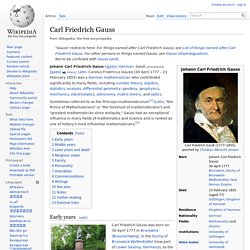
Sometimes referred to as the Princeps mathematicorum[1] (Latin, "the Prince of Mathematicians" or "the foremost of mathematicians") and "greatest mathematician since antiquity," Gauss had an exceptional influence in many fields of mathematics and science and is ranked as one of history's most influential mathematicians.[2] Early years[edit] Gauss was a child prodigy. There are many anecdotes about his precocity while a toddler, and he made his first ground-breaking mathematical discoveries while still a teenager. The year 1796 was most productive for both Gauss and number theory. Leonhard Euler. Swiss mathematician, physicist, and engineer Leonhard Euler ( OY-lər;[2] German: [ˈɔʏlɐ] ( Euler was one of the most eminent mathematicians of the 18th century and is held to be one of the greatest in history.
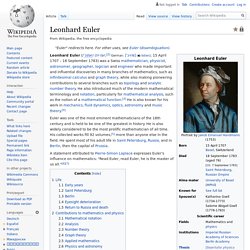
He is also widely considered to be the most prolific mathematician of all time. His collected works fill 92 volumes,[5] more than anyone else in the field. The Thirty Greatest Mathematicians. Click for a discussion of certain omissions.

Please send me e-mail if you believe there's a major flaw in my rankings (or an error in any of the biographies). Obviously the relative ranks of, say Fibonacci and Ramanujan, will never satisfy everyone since the reasons for their "greatness" are different. I'm sure I've overlooked great mathematicians who obviously belong on this list. Please e-mail and tell me! Following are the top mathematicians in chronological (birth-year) order. Earliest mathematicians Little is known of the earliest mathematics, but the famous Ishango Bone from Early Stone-Age Africa has tally marks suggesting arithmetic. Early Vedic mathematicians The greatest mathematics before the Golden Age of Greece was in India's early Vedic (Hindu) civilization.
Top.