

GALILÉE, MON CONTEMPORAIN : UNE PRÉSENTATION VIDÉO POUR LA FÊTE DE LA SCIENCE. [Rediffusion d’un billet publié en octobre 2020] Le 8 novembre 2020 - Ecrit par Charles Boubel Cette année une part de la fête de la science était à distance.
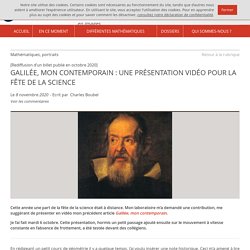
Mon laboratoire m’a demandé une contribution, me suggérant de présenter en vidéo mon précédent article Galilée, mon contemporain. Je l’ai fait mardi 6 octobre. Cette présentation, hormis un petit passage ajouté ensuite sur le mouvement à vitesse constante en l’absence de frottement, a été testée devant des collégiens. En rédigeant un petit cours de géométrie il y a quelque temps, j’ai voulu insérer une note historique. La créativité de Galilée, parfois totalement novatrice, son habileté expérimentale : il est malin, parfois rusé, sa rigueur et sa clarté.
Voici l’histoire : Notes. Bibliographie. [1a] Galileo Galilei, Dialogue sur les deux grands systèmes du monde. . [1b] Galileo Galilei, Discours concernant deux sciences nouvelles. Liens donnés à la fin dans l’appendice sur la LPR. La vie d’Évariste Galois. "La pensée d'Evariste Galois et le formalisme moderne" Extrait. Evariste Galois. Résumé A l ' occasion du bicentenaire de la naissance d ' Evariste Galois, ce film évoque la vie et l ' oeuvre d ' un des plus grands génies des mathématiques, dont la théorie a révolutionné les mathématiques et la physique modernes.
Des historiens et un chercheur évoquent le parcours de ce personnage dont la vie a été très brève. Evariste Galois, le mathématicien rejeté. Galois est certainement un des plus grands mathématiciens du monde.

Son apport, sans avoir été reconnu de son vivant à cause de l'incompréhension de ses contemporains, est immense. Galois sut mêler mathématiques et politique et sa vie est aujourd'hui entourée d'anecdotes qu'on ne peut ni valider ni réfuter comme son oral de Polytechnique. Même sa mort est énigmatique : certains pensent qu'il s'est battu par amour, d'autres qu'il a été victime d'un conflit royaliste. Une autre possibilité serait un suicide arrangé. ÉVARISTE GALOIS : ENFANCE D’UN GÉNIE MALHEUREUX. Il était une fois, dans la Grand’Rue du Bourg-la-Reine, à une dizaine de kilomètres au sud de Paris, une institution de jeunes gens dont l’origine remontait au delà de la Grande Révolution.

Cette dernière ne fut d’ailleurs pas étrangère à la prospérité de ce pensionnat, d’une part parce que la famille qui le tenait s’y rallia très vite, d’autre part parce que la plupart des collèges et autres pensionnats, tenus presque tous par des prêtres, étaient devenus suspects pour ceux qui n’avaient pas simplement disparu. Au tournant des années 1810, le grand-père céda sa pension à son fils cadet de 36 ans, Nicolas-Gabriel, qui devint un véritable fonctionnaire, le chef d’une institution de l’Université impériale. Nicolas-Gabriel était un homme du XVIIIe siècle, aimable et spirituel, en particulier amateur de poésie et profondément pénétré de philosophie.
Avenue Galois, Bourg-la-Reine Lycée Louis-le-Grand Cour d’honneur du lycée 1826-1827. MOOC ENS MATHÉMATIQUES ► Introduction à la théorie de Galois. Théorie de Galois (pour deg(P)>=5 peu probable d'exprimer les racines de P) Histoire d'un génie. Le mathématicien Évariste Galois. Décédé à 20 ans, a fondé la Théorie de Galois. La vie d’Évariste Galois. GALOIS EN MAISON DE SANTÉ (I)
Entre la prison pour cause de militantisme républicain radical et un duel aussi célèbre que fatal, le mathématicien Évariste Galois a séjourné en maison de santé.

Il y aurait connu une brève affaire sentimentale avec une certaine Stéphanie, peut-être Stéphanie Poterin du Motel, une Stéphanie qui, « infâme coquette », aurait précipité sa fin sur le terrain. Il convient donc d’examiner ce séjour avec attention... Son existence n’est attestée que par une ultime et laconique mention portée sur l’acte d’écrou de Galois : « Transféré à la maison de santé du S.
Faultrier, rue de l’Oursine n° 86, le 16 mars 1832 [1] ». Galois en maison de sante (II) Le mathématicien Évariste Galois est mort des suites d’un duel aussi célèbre qu’obscur, alors qu’il sortait tout juste de la prison où l’avait jeté son militantisme républicain radical.

C’est du moins ce qu’affirme son premier biographe (« La mort l’attendait à la sortie [1] »), son deuxième biographe (« Il venait d’en sortir [2] ») ou même le poète Gérard de Nerval (« le lendemain de sa mise en liberté [3] »). Ces témoignages sont imagés, au moins sur le lieu : comme nous l’avons vu dans un précédent billet, l’acte d’écrou de Galois montre qu’il a exécuté la fin de sa peine en maison de santé, et non en prison à proprement parler.
ÉVARISTE GALOIS ET ERNEST DUCHÂTELET VS BRUTUS MARCELLE ET AL. Le 14 juillet 1831, alors qu’ils s’apprêtent à fêter la prise de la Bastille en assistant à la plantation d’un « arbre de la liberté », Galois et un de ses amis républicains sont interpellés par les forces de l’ordre aux abords du Pont-Neuf.

Un rapport conservé dans les archives de la police témoigne ainsi de l’événement : Duchâtelet Ernest, et un autre individu qui n’a pas voulu dire son nom, ont été arrêtés par la garde nationale et une patrouille de la garde municipale ; ils étaient porteurs de carabines chargées et amorcées, et l’un d’un poignard et d’un moule à balles. Ils ont été conduits à la préfecture de police [1]. Galois était déjà connu des services de police. Le 9 mai précédent, lors d’un banquet républicain, il avait porté un toast régicide en exhibant un poignard justement, ce qui lui avait valu une première arrestation et un premier procès, dont il était sorti acquitté.
M. La-vie-d-Evariste-Galois-II. Il y a eu un autre Évariste Galois.
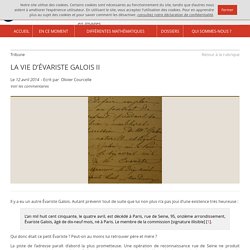
Autant prévenir tout de suite que lui non plus n’a pas joui d’une existence très heureuse : L’an mil huit cent cinquante, le quatre avril, est décédé à Paris, rue de Seine, 95, onzième arrondissement, Évariste Galois, âgé de dix-neuf mois, né à Paris. Le membre de la commission [signature illisible] [1]. Qui donc était ce petit Évariste ? Peut-on au moins lui retrouver père et mère ? La piste de l’adresse paraît d’abord la plus prometteuse. PREMIERS ET DERNIERS INSTANTS DE GALOIS. Je me demande si la date de naissance d’Évariste Galois traditionnellement indiquée dans les dictionnaires et les encyclopédies est bien exacte… La déclaration d’état-civil, dressée le 26 octobre 1811 à une heure de l’après-midi par le maire de Bourg-la-Reine, mentionne que l’enfant est « né le jour d’hier à une heure du matin » [1].
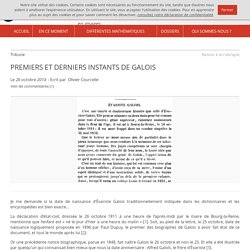
Soit, au pied de la lettre, le 25 octobre, date de naissance logiquement proposée en 1896 par Paul Dupuy, le premier des biographes de Galois à avoir fait état de ce document, et tout le monde après lui [2]. Or une précédente notice biographique, parue en 1848, fait naître Galois le 26 octobre et non le 25. Et elle a été illustrée par quelqu’un qui connaissait bien mieux que nous la date anniversaire : Alfred Galois, le frère d’Évariste [3]. Cette circonstance invite donc à se demander si par « hier à une heure du matin » il ne fallait pas comprendre en réalité « cette nuit ». Bon… Au cœur de l'histoire: La vie fulgurante du mathématicien Évariste Galois (Franck Ferrand)
Evariste Galois, mathématicien romantique. Avec nos partenaires, nous traitons vos données pour les finalités suivantes : le fonctionnement du site, la mesure d'audience et web analyse, la personnalisation, la publicité et le ciblage, les publicités et contenus personnalisés, la mesure de performance des publicités et du contenu, le développement de produit, l'activation des fonctionnalités des réseaux sociaux.
Vos préférences seront conservées pendant une durée de 6 mois. Retour sur un génie mathématicien (E. Galois) Nous revenons à nouveau sur Évariste Galois, mort à 21 ans, tué au cours d’un duel en 1832 tant la figure et l’œuvre de ce mathématicien est riche et profondes. Surtout qu’un ouvrage très récent, celui de Caroline Ehrhardt, approfondi encore la connaissance de ce génie.
D’où cette suite de questions : Comment a-t-il pu devenir célèbre au point qu’une théorie algébrique porte son nom ? Pourquoi çà n’est qu’une dizaine d’années après sa mort prématurée que ses travaux mathématiciens furent publiés et reconnus ? Qu’elles sont les pratiques des mathématiques, notamment dans le milieu scolaire où se forma Galois ? Ou encore, quels étaient les sujets d’examens à l’École polytechnique où Galois fut un candidat malheureux avant de se rabattre sur l’École normale ? Théorie de Galois "artistique" L’ALIGNEMENT DE GALOIS. La ligne B du RER est sans doute la plus mathématicienne des lignes de transport en commun de l’agglomération parisienne, si ce n’est de la France, sinon du monde. Un billet, que dis-je un livre, que dis-je une encyclopédie ne suffirait sans doute pas à chanter ce grand chemin de fer qui, pour sa seule partie sud, partant de Saint-Michel-Notre Dame ou Luxembourg, autant dire le Quartier latin, traverse de riants environs jalonnés d’une pléthore d’institutions ou de lieux diversement attachés aux mathématiques : l’École polytechnique, la maison de campagne de Poincaré, l’Institut des hautes études scientifiques, l’Université Paris-Sud… Il y en a tant, en vérité, qu’en citer un, c’est en oublier dix !
Je me propose pour ma part de recourir au plan du RER B pour pointer et visualiser un alignement remarquable concernant Évariste Galois, mathématicien célèbre, entre autres pour sa mort à vingt ans des suites d’un duel aux circonstances obscures. Alors pourquoi en faire toute une histoire ? Evariste Galois par Alain Connes. BG-Evariste Galois - Free. EVARISTE GALOIS ET LA THÉORIE DE L’AMBIGUÏTÉ. Piste verte Le 8 mars 2012 - Ecrit par Alain Connes Cet article a été écrit en partenariat avec Bicentenaire de la naissance d’Évariste Galois Cette vidéo reprend l’enregistrement audio et les transparents d’une conférence à l’Académie des Sciences le mardi 29 novembre 2011. Le début de la conférence est une piste verte mais le conférencier ne tarde pas à convier l’auditeur à sortir des pistes balisées....
L’un des aspects des idées de Galois qui s’est imposé le plus facilement parmi les outils conceptuels des scientifiques de notre époque, est celui de groupe de symétrie. Mémoire sur les conditions de résolubilité des équations par radicaux. Le Mémoire sur les conditions de résolubilité des équations par radicaux a été déposé par Évariste Galois à l’Académie des sciences en janvier 1831, soit un an avant sa mort à l’âge de vingt-et-un ans. Il s’agit de la troisième version des recherches de Galois à ce sujet : les deux premiers manuscrits, précédemment communiqués à l’Académie, avaient été perdus. Ce dernier travail n’a pas reçu l’approbation de l’Académie, malgré un rapport plutôt encourageant où Poisson et Lacroix invitaient le jeune mathématicien à poursuivre ses recherches en vue de parfaire ses résultats. Évariste Galois (Alexandre Astruc 1965) Evariste Galois (extrait) LE DUEL DE GALOIS. Le 29 mai 1832, à la veille du célèbre duel qui allait lui coûter la vie, le mathématicien Évariste Galois résume ses travaux encore inédits dans une lettre adressée à son ami Auguste Chevalier...
Il la clôt par deux souhaits : que sa lettre soit publiée dans la Revue encyclopédique, un magazine scientifique d’intérêt général, et, plus accessoirement pour nous, que Gauss et Jacobi, deux sommités allemandes, soient priés de donner leur avis sur l’importance des résultats auxquels il est parvenu.
Chevalier ne se contentera pas de respecter ces dernières volontés : il rédigera en prime une notice biographique sur son ami, par ailleurs militant républicain révolutionnaire, qu’il fera paraître avec la « lettre testament » dans la Revue encyclopédique [1]. Ces deux lettres renferment les seules bribes d’informations aujourd’hui connues données par Galois lui-même sur le duel fatal.
C’est dans la première d’entre elles, notamment, qu’il déclare mourir « victime d’une infâme coquette ». IL Y A CENT QUARANTE ANS : LA MORT DE GALOIS. Mais qui a tué Evariste Galois CMH#7. [PODCAST - Le Jour J - E01 ] Le testament d'Evariste Galois, mathématicien maudit. VERS UNE LÉGENDE D’ÉVARISTE GALOIS. Le 15 avril 1906, paraît dans la revue Mercure de France une étude littéraire intitulée « Le double Rimbaud ».
Son auteur, Victor Segalen (1878-1919), médecin de marine et poète [1], s’interroge sur le renoncement de Rimbaud à l’écriture malgré la reconnaissance de ses pairs. Evariste Galois, un candidat à l’Ecole préparatoire en 1829. Cours galois. Systèmes différentiels linéaires et théorie de Galois différentielle effective Cours JNCF2020 Cluzeau. Les "équations de la géométrie" : vers une compréhension intuitive de la théorie de Galois (1847-1892) - WebTV Université de Lille. Werner et Evariste, par Claude Aslangul. Deux prénoms qui sonnent comme deux légendes, deux personnages aux destins fort différents mais que rapproche un génie leur ayant permis de poser des jalons décisifs et ainsi permettre une prodigieuse avancée de la connaissance.
Evariste et Werner, plutôt, pour respecter la chronologie. Le premier, mort dans des conditions qui demeurent en partie mystérieuses, foudroyé en pleine jeunesse lors d’un combat imbécile et ayant tout juste eu le temps, la veille, de rédiger à nouveau un mémoire fondamental malencontreusement égaré quand il ne fut pas tout simplement jugé indigne d’intérêt.
A moins que sa lumineuse intelligence n’ait été considérée comme un risque pour l’aura de certains. Biographie de Francis Galton. Sir Francis Galton est un anthropologue, explorateur, géographe, météréologue et statisticien(!) Galton Francis. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges. Planche de Galton. Planches de Galton. Martin Gardner. Signature. René Gateaux. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges. Mathématiques : Carl Friedrich Gauss par Etienne Ghys. Gauss, entre classicisme et modernité. Carl Friedrich Gauss naît le 30 avril 1777 à Brunswick dans une famille pauvre. Gauss est très précoce : à 3 ans, il apprend seul à lire et compter.
□ La légende du petit Gauss / Maths C qui ? #7. Imaginary Numbers Are Real [Part 1: Introduction] La 1ère démonstration de Gauss du théorème fondamental de l' Algèbre. 3 Gauss. Mathématiques/sciences - Mathemathieu. Les Génies de la Sciences n° 36 - Août 2008. A (very) Brief History of Carl Friedrich Gauss. Gauss (Gauß) Karl Friedrich. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges. Méthode d'intégration par les points de Gauss (pour les polynômes)
Bost Jean-Benoit - "C.-F. Gauss et les débuts de la théorie des nombres moderne" - 2012. L'arithmétique de Gauss. Carl Friedrich Gauss. □ Théorème de d'Alembert-Gauss : définition et explications. 3 dm4 sommeNpremiersEntiers Gauss 2 2010. Méthode du pivot de Gauss. Systèmes linéaires - pivot de Gauss. Méthode du pivot de Gauss. Rappel de cours Matrice 3 : Méthode de Gauss. Courbe de Gauss - Etude complète (parité, max, concavité, limites,...) - Exponentielles. Courbure de Gauss. Les Expériences de Dr Nozman - Science & Vie TV. Géométrie différentielle, 19.3.3.1 Courbure de Gauss d'une surface. Théorème de Gauss-Bonnet diaporama CM S5. Theorema Egregium de Gauss. Le lemme de Gauss. Gauss professeur de Riemann. Baratier. Bost Jean-Benoit - "C.-F. Gauss et les débuts de la théorie des nombres moderne" - 2012.
Israel Gelfand. Joseph Diez Gergonne. Théorème de Ceva-Gergonne-Nagel QUELQUES MOTS SUR LES FIGURES SANS PAROLES… II. Sophie Germain. Sophie Germain : les mathématiques au féminin. Conférence d'Anne Boyé (à des élèves de 6e) parle Sophie Germain. Appli identité remarquables Sophie Germain. Sophie Germain : une pionnière enfin reconnue. Femmes scientifiques #16 - Sophie Germain.
Baptiste Chantraine - Le théorème de Girard pour les triangles sphériques. La formule de Girard. Baptiste Chantraine - Le théorème de Girard pour les triangles sphériques. Jean Giraud 1. Jean Giraud 2. Biographie de Kurt Gödel. Gödel Kurt Friedrich. Kurt GÖDEL. Godel mai08. Les théorèmes d'incomplétude de Gödel — Science étonnante #37. Le théorème d'incomplétude de Godel - PS n°92. A (very) Brief History of Kurt Gödel. Kurt Gödel : l'incomplétude. La conjecture de Goldbach. Les théorèmes d’incomplétude de Gödel. Le théorème d’incomplétude de Gödel. Biographie de Christian Goldbach. Goldbach.