

Quaternion Powers - Math and Physics. Version 1.2, February, 2003 Updates 1.2A minor correction with the formula of converting from Quat to Axis.
The scale is missing a square root. Thanks to Shi for pointing that out. From version 1.0 - 1.1The norm of a quaternion should be the square root of the q.q. || u+v || <= || u || + || v || is violated for the previous definition of the magnitude. The code in the samples are updated as well. Foreword To me, the term 'Quaternion' sounds out of this world, like some term from quantum theory about dark matter, having dark secret powers. Why use Quaternions? To answer the question, let's first discuss some common orientation implementations. Euler representation This is by far the simplest method to implement orientation. X, y, z <-- angle to rotate around global coordinate axis that vary between 0 and 360 degrees (or 0 - 2pi). Note: The rotations are specified with respect to the global coordinate axis frame. Angle Axis representation Why are these representations bad?
Gimbal Lock q=[ w,v ] where. Quaternions.pdf. Understanding Quaternions. 1.
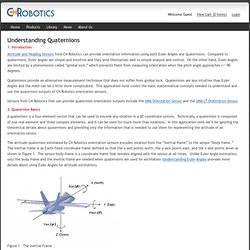
Introduction Attitude and Heading Sensors from CH Robotics can provide orientation information using both Euler Angles and Quaternions. Compared to quaternions, Euler Angles are simple and intuitive and they lend themselves well to simple analysis and control. On the other hand, Euler Angles are limited by a phenomenon called “gimbal lock,” which prevents them from measuring orientation when the pitch angle approaches +/- 90 degrees. Quaternions provide an alternative measurement technique that does not suffer from gimbal lock. Sensors from CH Robotics that can provide quaternion orientation outputs include the UM6 Orientation Sensor and the UM6-LT Orientation Sensor. 2. A quaternion is a four-element vector that can be used to encode any rotation in a 3D coordinate system. The attitude quaternion estimated by CH Robotics orientation sensors encodes rotation from the “inertial frame” to the sensor “body frame.” Figure 1 – The Inertial Frame Let the vector where.
Tutorial 17 : Rotations. This tutorial goes a bit outside the scope of OpenGL, but nevertheless tackles a very common problem: how to represent rotations ?
In Tutorial 3 – Matrices, we learnt that matrices are able to rotate a point around a specific axis. While matrices are a neat way to transform vertices, handling matrices is difficult: for instance, getting the rotation axis from the final matrix is quite tricky. We will present the two most common ways to represent rotation: Euler angles and Quaternions. Most importantly, we will explain why you should probably use Quaternions. While reading articles on rotations, you might get confused because of the vocabulary. An orientation is a state: “the object’s orientation is…”A rotation is an operation: “Apply this rotation to the object” That is, when you apply a rotation, you change the orientation. Conversion Quaternion to Euler.
Equations heading = atan2(2*qy*qw-2*qx*qz , 1 - 2*qy2 - 2*qz2) attitude = asin(2*qx*qy + 2*qz*qw) bank = atan2(2*qx*qw-2*qy*qz , 1 - 2*qx2 - 2*qz2)

Understanding Quaternions. Understanding Quaternions In this article I will attempt to explain the concept of Quaternions in an easy to understand way.
I will explain how you might visualize a Quaternion as well as explain the different operations that can be applied to quaternions. I will also compare applications of matrices, euler angles, and quaternions and try to explain when you would want to use quaterions instead of Euler angles or matrices and when you would not. DISCLAIMER: You cannot fully understand quaternions in just 45 minutes. This article is extremely math intensive and is not intended for the weak-hearted. In computer graphics, we use transformation matrices to express a position in space (translation) as well as its orientation in space (rotation). In this article, I will not discuss the details of transformation matrices. In this article, I want to discuss an alternative method of describing the orientation of an object (rotation) in space using quaternions.
The imaginary number has the form: or.