

Triangle. Triangle = Tri (trois) + Angle Types de triangles Diagramme d'Euler des types de triangles, utilisant la définition que les triangles isocèles ont au moins 2 côtés égaux (c'est-à-dire que les triangles équilatéraux sont isocèles).
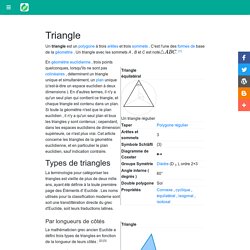
La terminologie pour catégoriser les triangles est vieille de plus de deux mille ans, ayant été définie à la toute première page des Éléments d' Euclide . Les noms utilisés pour la classification moderne sont soit une translittération directe du grec d'Euclide, soit leurs traductions latines. Par longueurs de côtés.
Triangle quelconque. Triangles remarquables. Vivent les cas d’égalité ! Avant de quitter Euclide, remarquons que dans toutes les propositions citées nous retrouvons souvent le mot « égal ».
Que recouvre-t-il pour Euclide ? La première réponse est qu’on n’en sait rien car la notion d’ « égalité » n’est pas définie d’une manière générale dans les Éléments. Les six premières notions communes qui fixent ce qu’on peut faire avec des « choses » égales (exemple NC1 : les choses égales à une même chose sont égales entre elles) apparaissent comme des axiomes de l’égalité et valent pour des grandeurs. Par exemple, nous avons vu dans la proposition 35 deux parallélogrammes équivalents en aires qu’Euclide nomme égaux et qui ne sont pas superposables. Pour Euclide l’égalité des triangles et des parallélogrammes mentionnés serait donc une égalité de grandeurs. 2.
Relations métriques dans le triangle rectangle. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges.

Théorème de Ceva. Les droites (AD), (BE) et (CF) sont concourantes ou parallèles si et seulement si Il doit son nom au mathématicien italien Giovanni Ceva qui, quelques années après le mathématicien espagnol José Zaragoza, en énonce et démontre une version dans le De lineis rectis se invicem secantibus statica constructio en 1678[1].
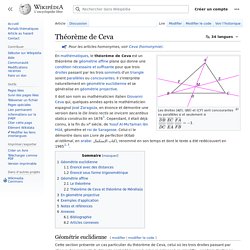
Cependant, il était déjà connu, à la fin du XIe siècle, de Yusuf Al-Mu'taman ibn Hűd, géomètre et roi de Saragosse. Celui-ci le démontre dans son Livre de perfection (Kitab al-Istikmal, en arabe: كتاب الإستكمال), renommé en son temps et dont le texte a été redécouvert en 1985[2],[3]. Géométrie euclidienne[modifier | modifier le code] Céviennes du triangle et théorème de Stewart. LES TRIANGLES ÉQUILATÉRAUX N’EXISTENT PAS.
En fait, ce qui n’existe pas, ce sont les triangles équilatéraux sur un écran d’ordinateur.
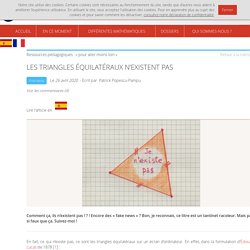
En effet, dans la formulation d’Édouard Lucas de 1878 [1] : Théorème : « Les sommets ou les centres d’un échiquier quelconque ne sont jamais situés aux sommets d’un triangle équilatéral. » Autrement dit, pour ce qui est de la partie de l’énoncé concernant les sommets de l’échiquier, il n’existe pas de triangle équilatéral dont les sommets soient des sommets d’un quadrillage à mailles carrées. On en déduit la partie concernant les centres des cases de l’échiquier, puisqu’il s’agit des sommets d’un second quadrillage à mailles carrées, de tailles égales à celles du quadrillage initial, comme on le voit sur la figure suivante, représentant certains des sommets du second quadrillage, un triangle dont les sommets sont choisis parmi eux, et l’une des nouvelles cases : Triangles Kentzel. R7. 4e-Olympique-Couper un triangle en deux parties égales. Couper un triangles en 2 parties égales.
88. 5e-Orthocentre cherche triangle d'origine. Triangles. Le théorème de Viviani - Automaths #16. Théorème de Viviani. Théorème de Viviani. Pourcentages. Notes sur un triangle par René Jodoin. Math.ing : les triangles et l’astronomie. Triangle de Calabi. GEOMATIQUE : Construire le puzzle de Dudeney. Triangles have a Magic Highway - Numberphile. Triangle Centres and the Euler Line (extra footage) Barbara Schapira - Triangles et géométries. Baptiste Chantraine - Le théorème de Girard pour les triangles sphériques. La formule de Girard. Vous avez manqué la dernière vidéo qui parle de géométrie sphérique ?
Il n’est jamais trop tard pour aller la regarder ! Dans cette vidéo, je mentionne une propriété très importante en géométrie sphérique : la somme des angles d’un triangle y est toujours supérieure à 180 degrés (ou plutôt π radians, puisque nous utiliserons plutôt cette unité d’angle pour la suite). De combien ? Potentiellement beaucoup, il n’y a pas de valeur fixe. Cette somme peut valoir entre π, pour un triangle d’aire nulle à 3π, pour une hémisphère… ce qui nous prive d’un beau résultat.
Mais de belles formules, il n’en manque pas, cependant ! Prenez trois points A, B et C sur une sphère. En faisant de même avec B et C, puis avec A et C, on délimite ainsi une zone qui est ce que l’on nomme tout simplement un triangle sphérique. Nous appellerons alors α l’angle situé au sommet A, β celui situé sur le sommet B et γ celui situé sur le sommet C, ces angles étant exprimés en radians. Regardons pour commencer l’angle α . Des triangles à l’infini.
A Chinese 5th Grader Solved This In Just 1 Minute! HARD Geometry Problem. Tesseler Les triangles sont ma forme préférée. Triangles are my favorite shape Le 22 novembre 2017 - Ecrit par Aurélien Alvarez Triangles are my favorite shapeThree points where two lines meetToe to toe, back to back, let’s go, my love ; it’s very late’Til morning comes, let’s tessellate [1] Ce dimanche matin, j’ai eu le plaisir de découvrir une version contemporaine et en vidéo de cette fresque [2].
Depuis, j’écoute alt-J, un groupe de rock indépendant britannique 👌. Enjoy ! Article édité par Emmanuel Jacob Notes. Triangulation - Maillage. Coordonnées barycentriques. Triangle de reuleaux. TRIANGLE de REULEAUX Triangle équilatéral flanqués de segments de cercles.

Sur chaque côté, on dessine le segment de cercle avec le sommet opposé comme centre et la longueur du côté comme rayon. Largueur ou diamètre d'une figure. Le triangle recourbé de Reuleaux / Études // Études Mathématiques. Celui–ci c’est un mécanisme de projection de films.
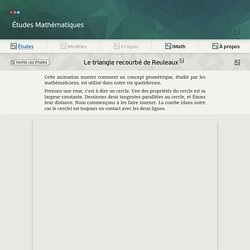
Le moteur d’un appareil pareil, en fait, génère une rotation continue autour d’un axe, mais afin d’avoir des images nettes sur l’écran, chaque image doit rester un moment immobile, tandis que la transition d’un cadre à l’autre doit se dérouler dans un temps beaucoup plus court. Tout cela 18 fois par seconde. Ce problème est effectivement résolu simplement par un mécanisme qui est basé sur le triangle de Reuleaux, inscrite dans un carré, et un double parallélogramme, ce qui empêche au carré de s’incliner. En fait, comme les longueurs des côtés opposés sont égaux, l’élément central pendant les mouvements reste parallèle à la base et le côté du carré reste toujours parallèle à l’élément central.
Inventer la roue / Études // Études Mathématiques. HISTOIRE DES ARTS: LE TRIANGLE DE REULEAUX. Faires des trous carrés / Études // Études Mathématiques. Si maintenant vous avez le foret d’une perceuse ayant la forme du triangle de Reuleaux, alors vous pouvez percer des trous carrés un peu «arrondis» aux coins, mais avec les côtés parfaitement droits!
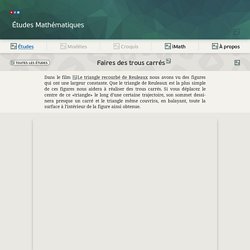
Il reste à construire une telle perceuse... Ou plutôt, il n’est pas compliqué de construire le foret en soi, il suffit qu’il aie une section similaire au triangle de Reuleaux, avec les arêtes vives en correspondance des sommet du triangle. La seule difficulté est, comme indiqué précédemment, que la trajectoire du centre du triangle doit être composé de quatre arcs d’ellipses. A vue de nez, cette courbe ressemble beaucoup à un cercle, et même mathématiquement est très proche de lui, mais ce n’est pas un cercle, tandis que toute excentrique (obtenue par un cercle dont le centre se déplace sur un autre cercle de rayon différent) utilisée dans les mécanismes techniques, donne un mouvement qui est strictement circulaire. Nous allons utiliser une autre construction. Point de Torricelli dans le triangle.
Pointe de Steiner (triangle) En géométrie triangulaire , le point de Steiner est un point particulier associé à un triangle . [1] Il est un centre de triangle [2] et il est désigné comme étant le centre X (99) dans Clark Kimberling du nombre de kimberling . Jakob Steiner (1796-1863), mathématicien suisse, a décrit ce point en 1826. Le point a reçu le nom de Steiner par Joseph Neuberg en 1886. [2] [3] Définition.
Steiner - Fermat - Torricelli. Tous les triangles sont équilatéraux ! C’est un grand classique, mais après ce que je vous ai infligé la semaine dernière, je me suis dit qu’un peu de repos ne ferait de mal à personne ! Donc nous allons démontrer que tous les triangles sont équilatéraux. Rien que ça ! Et puisqu’on démontre que tous les triangles sont équilatéraux, il s’ensuit que 1+1=3, que les maths sont contradictoires, que Gödel l’avait prédit et que je suis le pape. La démonstration.