

Book. Japanese Multiplication Method. Trigonometry - Heliocentrism and Geocentrism. ≈ 350 BC, Aristotle Aristotle, a pupil of Plato, becomes the tutor of Alexander the Great.
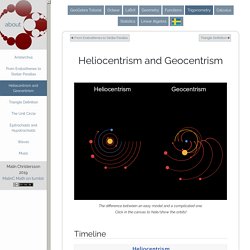
Aristotle's views of the world shape science for centuries. His influence lasts until the enlightenment. In his book On the Heavens (part 14), Aristotle asserts that: From these considerations then it is clear that the earth does not move and does not lie elsewhere than at the centre. ≈ 250 BC, Aristarchus Aristarchus estimates the size of the sun to be much larger than the size of the earth. . ≈ 250 BC, Archimedes In The Sand-Reckoner, Archimedes estimates the number of sand corns in the universe using the heliocentric model of Aristarchus. ≈ 150 AD, Ptolemy In his book Almagest, Ptolemy introduces so called epicycles to explain planetary motions, based on the assumption that the earth is at the centre and does not move. 1543, Nicholaus Copernicus 1572, Tycho Brahe Tycho Brahe observes a star being born and publishes his observation in De nova stella. 1609, Johannes Kepler 1616, Roman Inquisition.
Ericvilas: darkado: memecucker: ...
The Wood between Worlds: Virtual Aristotelian Physics. I spent several hours the other day looking up some sort of reference to a computer simulation of Aristotelian physics.

The thought came to me in connection to fantasy worlds. Good fantasy authors will create their own fictional worlds with different histories, cultures, languages, and religions, similar to Tolkien's Lord of the Rings. Lately authors have started going kind of crazy, and have been experimenting with alternative physics, like flat earths and sentient quanta. I was thinking, why not Aristotelian physics? Is it that impossible? The basic and most central idea in Aristotle's conception of physics is that he was an ancient Greek philosopher completely removed from my modern view of mathematical science and more interested in teleology and such.
This means that when you stop applying a force to something, it stops moving. Another principle is that objects can only have one "kind" of motion at a time - that is, in straight lines. I ramble. Dendritic-trees: copperbadge: ... - frank the shark. Downtroddendeity: downtroddendeity: I have spent the last 8 horrified/fascinated hours digging down the rabbit hole of a famous Cornell University marketing professor’s fake-research empire crumbling as soon as anyone actually looked at his methods and it just keeps getting crazier the more I look.

Among other highlights, the Joy of Cooking copyright holders actually caught him before the scientific community did. For reference: this is a dude who has mostly worked in the psychology of food and nutrition. He got famous for publishing a whole lot of catchy studies about what makes people eat more or less, and you’ve probably heard some of his stuff that got turned into huge media soundbites. He published a paper that requires you not to notice that the amount of food eaten by children and the amount not eaten add up to more than the amount served in all three categories. alwaysatomicconniseur replied to your post: I have spent the last 8 horrified/fascinated hours… Please tell me more.
How Probability Is Perceived . . . I ran across this explanation of Probability as seen by different professions at Sam Wang’s Princeton Consortium and tracked it down to Ben Orin’s Math with Bad Drawings blog.

A little about Ben and his blog as told by himself: “This blog is about the things I like. It’s also about the things I can’t do. Unreasonable Effectiveness of Knot Theory. Editor's note: This article was originally published as “Unreasonable Effectiveness” in Plus Magazine, a free online publication of the Millennium Mathematics Project based at the Centre for Mathematical Sciences, Cambridge University, England.

We thank the author, Mario Livio, and Plus editors Marianne Freiberger and Rachel Thomas for allowing Convergence to republish the article. In 1960, physics Nobel Laureate Eugene Wigner wrote a famous article entitled "The Unreasonable Effectiveness of Mathematics in the Natural Sciences. " In this article, Wigner referred to the uncanny ability of mathematics not only to describe, but even to predict phenomena in the physical world. He wrote: Middle ages - Did the pope try to suppress the number zero? - History Stack Exchange. By using our site, you acknowledge that you have read and understand our Cookie Policy, Privacy Policy, and our Terms of Service.
History Stack Exchange is a question and answer site for historians and history buffs. It only takes a minute to sign up. Sign up to join this community Anybody can ask a question Anybody can answer The best answers are voted up and rise to the top Did the pope try to suppress the number zero? Ask Question Asked 7 years, 1 month ago Active 10 months ago Viewed 3k times This question shows research effort; it is useful and clear This question does not show any research effort; it is unclear or not useful Bookmark this question. Show activity on this post.